Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

. . . . O A B C D x y / / // // a) Xét \(\Delta OAD\) và \(\Delta OCB\) có:
OA = OC (gt)
\(\widehat{O}\) (chung)
OB = OD(gt)
Do đó: \(\Delta OAD=\Delta OCB\left(c-g-c\right)\)
=> AD = BC (hai cạnh tương ứng)
b) Vì \(\Delta OAD=\Delta OCB\left(cmt\right)\)
=> \(\widehat{OAD}=\widehat{OCB}\) (hai góc tương ứng)
mà :
\(\widehat{OAD}+\widehat{BAD}=180^0\) (kề bù)
\(\widehat{OCB}+\widehat{BCD}=180^0\) (kề bù)
=> \(\widehat{BAD}=\widehat{BCD}\) (đpcm)

a) Ta có: OD = OB + BD
OC=OA+AC
mà OA=OB; AC=BD
=>OD=OC
Xét 2 TG ODA và OCB;ta có:
OA-OB(gt); O:góc chung; OD=OC(cmt)
=>TG ODA= TG OCB(c.g.c)
=>AD=BC(2 cạnh tương ứng)
b. TG ODA=TG OCB=> góc C=góc D(2 góc tương ứng)
=>OAD=OBC(2 góc tương ứng)
Ta có: OAD+EAC=180
OBC+EBD=180
Từ (1) và (2)=> OAD+EAC=OBC+EBD=180
mà OAD=OBC(cmt)=>EAC=EBD
Xét 2 TG EAC và EBD; ta có:
AC=BD(gt); C=D(cmt); EAC=EBD(cmt)
=>TG EAC=TG EBD (g.c.g)
c. Vì TG EAC=TG EBD=> EA=EB(2 cạnh tương ứng)
Xét TG OBE và OAE, ta có:
OA=OB(gt); EA=EB(cmt); OE:cạnh chung
=>TG OBE=TG OAE(c.c.c)
=>BOE=EOA(2 cạnh tương ứng)
mà OE nằm giữa OA và OB=> OE là phân giác của góc xOy
Không pt đúng ko

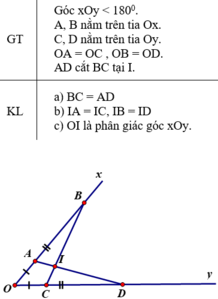
a) ΔAOD và ΔCOB có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
⇒ ΔAOD = ΔCOB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)

Ta có: ΔOIA và ΔOIC có
OI chung
IA = IC (chứng minh trên)
OA = OC (giả thiết)
ΔOIA = ΔOIC (c.c.c)

x O y A C B D
a) Xét ▲OAD và ▲OBC có :
OA = OB ( gt )
góc COD chung
OC = OD ( gt )
=> ▲OAD = ▲OBC ( c-g-c )
=> đpcm
b) Gọi giao điểm của BC và AD là M
Vì ▲OAD = ▲OBC ( c/m trên )
=> góc OCB = góc ODA ( 2 góc tương ứng )
Xét ▲ACM có góc MAC + góc ACM + góc CMA = 1800
Xét ▲BMD có góc BMD + góc MDB + góc DBM = 1800
Mà góc OCB = góc ODA ( c/m trên ) và góc CMA = góc BMD ( đối đỉnh )
=> góc CAM = góc MBD ( đpcm )

a) ∆OAD và ∆OCB có: OA= OC(gt)
ˆAODAOD^=ˆCOBCOB^(=ˆAA^)
OD=OB(gt)
Nên ∆OAD=∆OCB(c.g.c)
suy ra AD=BC.
b) ∆OAD=∆OCB(cmt)
Suy ra: ˆDD^= ˆBB^
ˆA1A1^=ˆC1C1^ => ˆA2A2^=ˆC2C2^
Do đó ∆AOE = ∆OCE(c .c.c)
suy ra: ˆOAEOAE^=ˆCOECOE^
vậy OE là tia phân giác của xOy.
b) ∆AEB= ∆CED(câu b) => EA=EC.
∆OAE và ∆OCE có: OA=OC(gt)
EA=EC(cmt)
OE là cạnh chung.
Nên ∆OAE=∆(OCE)(c .c.c)
suy ra: ˆAOEAOE^=ˆCOECOE^
vậy OE là tia phân giác của góc xOy.
 hoang phuong anh
hoang phuong anh