Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho góc AOB = 150 độ. Vẽ ra ngoài góc AOB hai tia OC và OD theo thứ tự vuông góc với OA và OB. Gọi Ox là phân giác của góc AOB, Oy là tia đối của tia Ox.
Yêu cầu:
a. Tính góc BOC b. So sánh góc XOC và góc YOB
Giải:
a. Ta có:
- Góc AOB = 150 độ
- Góc AOX = góc AOB/2 = 75 độ
- Góc AOC = 90 độ
Vì OA vuông góc với OC nên góc AOC và góc AOX là hai góc kề bù.
- Góc AOC + góc AOX = 180 độ
- Góc AOC + 75 độ = 180 độ
- Góc AOC = 105 độ
Vì OC vuông góc với OB nên góc AOC và góc BOC là hai góc kề bù.
- Góc AOC + góc BOC = 180 độ
- Góc BOC = 180 độ - 105 độ = 75 độ
Vậy, góc BOC = 75 độ.
b. Ta có:
- Góc XOC = góc AOX + góc AOC = 75 độ + 90 độ = 165 độ
- Góc YOB = 180 độ - góc XOC = 180 độ - 165 độ = 15 độ
Vì góc XOC > góc YOB nên góc XOC > góc YOB.
Kết luận:
- Góc BOC = 75 độ
- Góc XOC > góc YOB

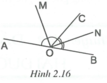
Ta có O M ⊥ O N ⇒ M O N ^ = 90 ° .
Tia OM là tia phân giác của góc AOC nên A O M ^ = M O C ^ .
Tia ON là tia phân giác của góc BOC nên B O N ^ = N O C ^ .
Xét tổng
A O C ^ + B O C ^ = 2 M O C ^ + 2 N O C ^ = 2 M O C ^ + N O C ^ = 2 M O N ^ = 2.90 ° = 180 ° .
Hai góc kề AOC và BOC có tổng bằng nên hai tia OA, OB đối nhau.
Đường trung trực – Hai góc có cạnh tương ứng vuông góc

Bài 1
x x' y y' O ) 1 2 3 4 m n
a
Ta có:
\(\widehat{O_1}=\widehat{O_2}=60^0\left(đ.đ\right)\)
\(\widehat{O_1}+\widehat{O_2}=180^0\Rightarrow\widehat{0_2}=180^0-\widehat{O_1}=180-60^0=120^0\)
\(\widehat{O_2}=\widehat{O_4}=120^0\left(đ.đ\right)\)
b
Ta có:
\(\widehat{x'Oy}=\widehat{y'Ox}\Rightarrow\frac{1}{2}\widehat{x'Oy}=\frac{1}{2}\widehat{y'Ox}\Rightarrow\widehat{yOn}=\widehat{xOm}\)
\(\widehat{x'Oy}+\widehat{yOx}=180^0\)
\(\Rightarrow2\cdot\widehat{yOn}+\widehat{yOx}=180^0\)
\(\Rightarrow\widehat{yOn}+\widehat{yOx}+\widehat{xOm}=180^0\)
\(\Rightarrowđpcm\)
Bài 2
A O B C D M
a
Ta có:
\(\widehat{BOD}=\widehat{AOC}=90^0\Rightarrow\widehat{BOC}+\widehat{COD}=\widehat{AOD}+\widehat{COD}\Rightarrow\widehat{BOC}=\widehat{AOD}\)
b
Ta có:
\(\widehat{BOM}=\widehat{BOC}+\widehat{COM}=\widehat{AOD}+\widehat{MOD}=\widehat{MOA}\)
Hiển nhiên OM nằm giữa \(\widehat{AOB}\) nên suy ra đpcm
ai làm dc giúp mih nha!!!