Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì AB là tiếp tuyến (O)
=> AB⊥OB
=> ABOˆABO^=900=900
Vì AC là tiếp tuyến (O)
=> AC⊥OC
=>ACOˆACO^ =900=900
Ta có: ABOˆ+ACOˆABO^+ACO^ =900+900=1800=900+900=1800
=> Tứ giác ABOC nội tiếp đường tròn. (theo dấu hiệu nhận biết tứ giác nội tiếp)
b) Vì tiếp tuyến AB cắt tiếp tuyến AC tại A
⇒{AB=ACBO=CO⇒{AB=ACBO=CO
⇒⇒ AO là đường trung trực ứng BC
⇒⇒ AO⊥BC ( mà E∈BC)
⇒⇒ BE⊥AO (đpcm)
Xét ΔABO có: ABOˆABO^ =900=900 (cmtrn)
BE⊥AO (cmtrn)
⇒⇒ Áp dụng hệ thức lượng trong tam giác vuông.
⇒⇒ AO⋅OE=OB2AO⋅OE=OB2 (mà OB=R)
⇒OA⋅OE=R2⇒OA⋅OE=R2 (đpcm)
c) Vì tiếp tuyến BP cắt tiếp tuyến PK tại P
⇒PB=PK⇒PB=PK
Vì tiếp tuyến KQ cắt tiếp tuyến QC tại Q
⇒KQ=QC⇒KQ=QC
Ta có: PAPQ=AP+PQ+AQPAPQ=AP+PQ+AQ =AP+PK+KQ+AQ=AP+PK+KQ+AQ
⇔PAPQ=(AP+PB)+(QC+AQ)⇔PAPQ=(AP+PB)+(QC+AQ)
⇔PAPQ=AB+AC⇔PAPQ=AB+AC
Vì AB+ACAB+AC không thay đổi khi K chuyển động trên cung nhỏ BC
⇒⇒ Chu vi tam giác AQP không thay đổi khi K thay đổi trên cung nhỏ BC (đpcm).
d) Tự CM: ΔMOP∼ΔNQOΔMOP∼ΔNQO
⇒MPNO=MONQ⇒MPNO=MONQ ⇔MP⋅NQ=MO⋅NO=MN2⋅MN2⇔MP⋅NQ=MO⋅NO=MN2⋅MN2
⇔MP⋅NQ=MN24⇔MP⋅NQ=MN24
⇔MN2=4⋅(MP⋅NQ)⇔MN2=4⋅(MP⋅NQ)
⇔MN=2⋅MN⋅NQ−−−−−−−−√⇔MN=2⋅MN⋅NQ
Áp dụng bđt Côshi ta có:
2⋅MP⋅NQ−−−−−−−−√≤MP+NQ2⋅MP⋅NQ≤MP+NQ
⇔MN≤MP+NQ⇔MN≤MP+NQ (đpcm).

Từ một điểm A nằm bên ngoài đường tròn ( O ), kẻ các tiếp tuyến AB, AC với đường tròn ( B,C là các tiếp điểm )
a) Chứng minh rằng ABOC là tứ giác nội tiếp
b)Cho bán kính đường tròn ( O ) bằng 3cm, độ dài đoạn thẳng OA bằng 5cm. Tính độ dài đoạn thẳng BC
c) Gọi ( K ) là đường tròn qua A và tiếp xúc với đường thẳng BC tạo C. Đường trknf (K) và đường tròn (O ) cắt nhau tại điểm thứ hai là M. Chứng minh rằng đường thẳng BM đi qua trung điểm của đoạn thẳng AC

a) Có goc BAC=90độ=>góc EAF=90độ
HE vuong goc voi AB =>góc HEA=90độ
HF vuong goc voi AC=>góc HFA=90độ
==>AEHF là hình chữ nhật
Có góc ABC=góc EHA
mà góc EHA= góc EFA
góc ABC+OAC=90 độ
=>góc OAC+góc AFE=90 độ =>OA vuông góc với EF
b)có góc PBA=góc PFA
góc APC=góc ABC
mà góc ABC= góc AFP
=>goca PBA= góc APE=>tam giác AEP đồng dạng vs APB (gg)
=>AP^2=AE.AB
mà AH^2=AE.AB
=>tam giac PAH cân
c)
Chứng minh tam giác DKC đồng dạng với tam giác DBA (g-g) , Suy ra DK.DA=DC.DB (1)
Chứng minh Tứ giác BEFC nội tiếp ( góc AEF = góc FCH cùng bắng với góc AHF )
Từ đó chứng minh hai tam giác DFC và DBE đồng dạng (g-g), Suy ra DF.DE=DC.DB (2)
Từ (1) và (2) suy ra DK.DA = DF.DE. Từ đó chứng minh tam giác DKF đồng dạng với DEA (theo trường hợp c-g-c)
Suy ra góc DKF = góc DEA
Suy ra tứ giác AEFK nội tiếp
d) chứng minh được OA vuông góc với PQ.
Suy ra cung AP=cung AQ. suy ra ˆADP=ˆACKADP^=ACK^
=> KFCD nội tiếp => ΔIFC∼ΔIDKΔIFC∼ΔIDK
=> IC.ID=IF.IK. rồi cm IH^2=IF.IK dựa vào tứ giác AKFH nội tiếp do tứ giác AEFK nội tiếp

1) Hình vẽ câu 1) đúng
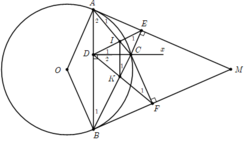
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B
_