Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ OH⊥EFOH⊥EF.
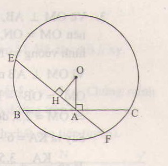
Xét tam giác HOA vuông tại H ta có OH<OA
Suy ra EF>BC..
Nhận xét. Trong các dây đi qua một điểm A ở trong đường tròn, dây vuông góc với OA là dây ngắn nhất.

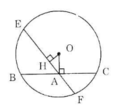
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).

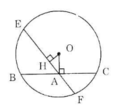
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).

giải:
Vẽ OH⊥EFOH⊥EF.
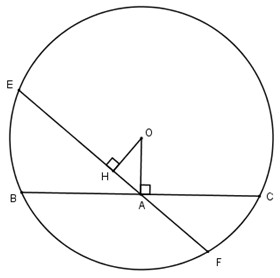
Xét tam giác HOA vuông tại H ta có:
OH<OAOH<OA.
Suy ra EF>BC.EF>BC.
Nhận xét. Trong các dây đi qua một điểm A ở trong đường tròn, dây vuông góc với OA là dây ngắn nhất.

C F E B D O A I J
a/
+ Vì BE // OD nên ta có ngay góc COD = góc DOB = góc OBE = góc OEB. Ta có :
góc COD + góc DOB + góc BOE = góc OBE + góc OEB + góc BOE = 180 độ
Vậy C,O,E thẳng hàng
+ Vì tam giác OCD cân tại O và OF vuông góc với CD nên OF đồng thời là đường phân giác => góc COF = góc FOD => Cung CF = cung FD
Do góc CED chắn cung CD và F là trung điểm của cung CD nên là đường phân giác góc CED.

a) Áp dụng định lí Pytago vào ΔABO vuông tại B, ta được:
\(OA^2=OB^2+AB^2\)
\(\Leftrightarrow AB^2=10^2-6^2=64\)
hay AB=8(cm)
b) Xét tứ giác OIBA có
\(\widehat{OIA}=\widehat{OBA}\left(=90^0\right)\)
Do đó: OIBA là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay O,I,B,A cùng thuộc 1 đường tròn
Tâm là trung điểm của OA