Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do AB là đường kính và D thuộc đường tròn
\(\Rightarrow\widehat{ADB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ADB}=90^0\) hay tam giác ADB vuông tại D
Xét tam với vuông ADB với đường cao DH, áp dụng hệ thức lượng ta có:
\(AD^2=AH.AB\)

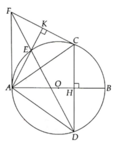
a, Học sinh tự chứng minh
b, DADB vuông tại D, có đường cao DH Þ A D 2 = AH.AB
c, E A C ^ = E D C ^ = 1 2 s đ E C ⏜ ; E A C ^ = K H C ^ (Tứ giác AKCH nội tiếp)
=> E D C ^ = K H C ^ => DF//HK (H là trung điểm DC nên K là trung điểm FC) => Đpcm

Giải thích các bước giải:
a.Ta có AK⊥CK,AH⊥CHAK⊥CK,AH⊥CH
→ˆAKC+ˆAHC=90o+90o=180o→AKC^+AHC^=90o+90o=180o
→A,H,C,K→A,H,C,K thuộc đường tròn đường kính AC
b. Vì ADAD là đường kính của (O)
→AB⊥BD→AB⊥BD
Mà BH⊥AD→AB2=AH.ADBH⊥AD→AB2=AH.AD
c. Vì BC⊥AD→B,CBC⊥AD→B,C đối xứng qua AD
→ˆABC=ˆACB→ABC^=ACB^
Mà AMCBAMCB nội tiếp (O)→ˆKMC=ˆABC(O)→KMC^=ABC^
→ˆNMK=ˆAMB=ˆACB=ˆABC=ˆKMC→NMK^=AMB^=ACB^=ABC^=KMC^
Xét 2 tam giác vuông ΔMKNΔMKN và ΔMKCΔMKC có:
KMKM chung
ˆNMK=ˆKMCNMK^=KMC^ (cmt)
⇒ΔMKN=ΔMKC⇒ΔMKN=ΔMKC (cạnh góc vuông-góc nhọn)
⇒KN=KC⇒AK⇒KN=KC⇒AK vừa là đường cao vừa là trung tuyến ΔANCΔANC
⇒ΔANC⇒ΔANC cân đỉnh AA.
d. Vì ΔACNΔACN cân tại A →AN=AC→AN=AC
Mà B,C đối xứng qua AD
→AC=AB→AN=AB→ΔABN→AC=AB→AN=AB→ΔABN cân đỉnh AA
Lấy E là trung điểm BN→AE⊥BN→AE⊥BN
→E→E là trung điểm BN
→SABN=12AE.BN=12AE.2BE=AE.BE≤AE2+BE22=AB22→SABN=12AE.BN=12AE.2BE=AE.BE≤AE2+BE22=AB22
Dấu = xảy ra khi AE=BE→ˆABE=45o→ˆABM=45oAE=BE→ABE^=45o→ABM^=45o


a: Xét tứ giác AHCK có \(\widehat{AHC}+\widehat{AKC}=90^0+90^0=180^0\)
nên AHCK là tứ giác nội tiếp
b: ta có: AHCK là tứ giác nội tiếp
=>\(\widehat{CHK}=\widehat{CAK}=\widehat{CAE}\left(1\right)\)
Xét (O) có
\(\widehat{CAE}\) là góc nội tiếp chắn cung CE
\(\widehat{CDE}\) là góc nội tiếp chắn cung CE
Do đó: \(\widehat{CAE}=\widehat{CDE}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{CHK}=\widehat{CDE}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên HK//DE