Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

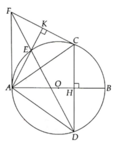
a, Học sinh tự chứng minh
b, DADB vuông tại D, có đường cao DH Þ A D 2 = AH.AB
c, E A C ^ = E D C ^ = 1 2 s đ E C ⏜ ; E A C ^ = K H C ^ (Tứ giác AKCH nội tiếp)
=> E D C ^ = K H C ^ => DF//HK (H là trung điểm DC nên K là trung điểm FC) => Đpcm

Do AB là đường kính và D thuộc đường tròn
\(\Rightarrow\widehat{ADB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{ADB}=90^0\) hay tam giác ADB vuông tại D
Xét tam với vuông ADB với đường cao DH, áp dụng hệ thức lượng ta có:
\(AD^2=AH.AB\)

Giải thích các bước giải:
a.Ta có AK⊥CK,AH⊥CHAK⊥CK,AH⊥CH
→ˆAKC+ˆAHC=90o+90o=180o→AKC^+AHC^=90o+90o=180o
→A,H,C,K→A,H,C,K thuộc đường tròn đường kính AC
b. Vì ADAD là đường kính của (O)
→AB⊥BD→AB⊥BD
Mà BH⊥AD→AB2=AH.ADBH⊥AD→AB2=AH.AD
c. Vì BC⊥AD→B,CBC⊥AD→B,C đối xứng qua AD
→ˆABC=ˆACB→ABC^=ACB^
Mà AMCBAMCB nội tiếp (O)→ˆKMC=ˆABC(O)→KMC^=ABC^
→ˆNMK=ˆAMB=ˆACB=ˆABC=ˆKMC→NMK^=AMB^=ACB^=ABC^=KMC^
Xét 2 tam giác vuông ΔMKNΔMKN và ΔMKCΔMKC có:
KMKM chung
ˆNMK=ˆKMCNMK^=KMC^ (cmt)
⇒ΔMKN=ΔMKC⇒ΔMKN=ΔMKC (cạnh góc vuông-góc nhọn)
⇒KN=KC⇒AK⇒KN=KC⇒AK vừa là đường cao vừa là trung tuyến ΔANCΔANC
⇒ΔANC⇒ΔANC cân đỉnh AA.
d. Vì ΔACNΔACN cân tại A →AN=AC→AN=AC
Mà B,C đối xứng qua AD
→AC=AB→AN=AB→ΔABN→AC=AB→AN=AB→ΔABN cân đỉnh AA
Lấy E là trung điểm BN→AE⊥BN→AE⊥BN
→E→E là trung điểm BN
→SABN=12AE.BN=12AE.2BE=AE.BE≤AE2+BE22=AB22→SABN=12AE.BN=12AE.2BE=AE.BE≤AE2+BE22=AB22
Dấu = xảy ra khi AE=BE→ˆABE=45o→ˆABM=45oAE=BE→ABE^=45o→ABM^=45o
