Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải 1 bài toán tương tự - Dài và khó
Giải toán: Bài hình trong đề thi HK2 Lớp 9 | Rất phức tạp. - YouTube


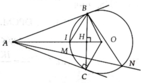
a) Hai tam giác vuông ABO và ACO có chung cạnh huyền AO nên A, B, O, C cùng thuộc đường tròn đường kính AO.
Vậy tứ giác ABOC là tứ giác nội tiếp.
b) Ta thấy ngay \(\Delta ABD\sim\Delta AEB\left(g-g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AE.AD=AB^2\)
Xét tam giác vuông ABO có BH là đường cao nên áp dụng hệ thức lượng ta có:
\(AH.AO=AB^2\)
Suy ra AD.AE = AH.AO
c) Ta có \(\widehat{PIK}+\widehat{IKQ}+\widehat{P}+\widehat{Q}=360^o\)
\(\Rightarrow2\left(\widehat{PIO}+\widehat{P}+\widehat{OKQ}\right)=360^o\)
\(\Rightarrow\widehat{PIO}+\widehat{P}+\widehat{OKQ}=180^o\)
Mặt khác \(\widehat{PIO}+\widehat{P}+\widehat{IOP}=180^o\)
\(\Rightarrow\widehat{IOP}=\widehat{OKQ}\Rightarrow\Delta PIO\sim\Delta QOK\)
\(\Rightarrow\frac{IP}{PO}=\frac{OQ}{KQ}\Rightarrow PI.KQ=PO^2\)
Sử dụng bất đẳng thức Cô-si ta có:
\(IP+KQ\ge2\sqrt{IP.KQ}=2\sqrt{OP^2}=PQ\)
acje cho hỏi 2 tam giác đồng dạng ở câu b là góc nào í chỉ ro rõ cho e với ạk

a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC
Lời giải:
1.
Vì $AB,AC$ là tiếp tuyến của $(O)$ nên \(AB\perp OB; AC\perp OC\)
\(\Rightarrow \widehat{ABO}=\widehat{ACO}=90^0\)
Tứ giác $ABOC$ có tổng hai góc đối nhau \(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\) nên $ABOC$ là tứ giác nội tiếp.
2.
Xét tam giác $ABE$ và $ADB$ có:
\(\widehat{A}\) chung
\(\widehat{ABE}=\widehat{ADB}\) (góc tạo bởi tiếp tuyến và dây cung thì bằng góc nội tiếp chắn cung đó, cụ thể ở đây là cung $BE$)
\(\Rightarrow \triangle ABE\sim \triangle ADB(g.g)\)
\(\Rightarrow \frac{AB}{AD}=\frac{AE}{AB}\Rightarrow AB^2=AE.AD(1)\)
Vì $AB=AC$ (t/c hai tiếp tuyến cắt nhau tại 1 điểm)
\(OB=OC=R\)
\(\Rightarrow OA\) là tiếp tuyến của $BC$. Do đó $OA\perp BC$ tại $H$
Xét tam giác vuông tại $B$ là $BAO$ có đường cao $AH$, theo hệ thức lượng trong tam giác vuông thì \(AB^2=AH.AO(2)\)
Từ \((1);(2)\Rightarrow AE.AD=AH.AO\)
Vậy ta có đpcm.
3.Gọi \(K=BI\cap (O)\)
Vì $I$ là tâm đường tròn nội tiếp $BCD$ nên $BI,CI$ là phân giác góc \(\widehat{CBD}, \widehat{BCD}\)
\(\Rightarrow \widehat{CBK}=\widehat{DBK}\)\(\Rightarrow \text{cung (DK)}=\text{cung (CK)}\Rightarrow DK=CK(*)\)
Lại có:
\(\widehat{ICK}=\widehat{ICD}+\widehat{DCK}=\widehat{ICD}+\widehat{DBK}\) (góc nt cùng chắn cung $DK$)
\(=\frac{\widehat{BCD}}{2}+\frac{\widehat{DBC}}{2}=\widehat{BCI}+\widehat{CBI}=\widehat{CIK}\)
Do đó tam giác $CIK$ cân tại $K$
\(\Rightarrow KC=KI(**)\)
Từ \((*); (**)\Rightarrow KC=KD=KI\) hay $K$ là tâm đường tròn ngoại tiếp tam giác $DCI$
Mà $K\in (O)$ nên ta có đpcm.
Hình vẽ: