Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x C A O B K y D
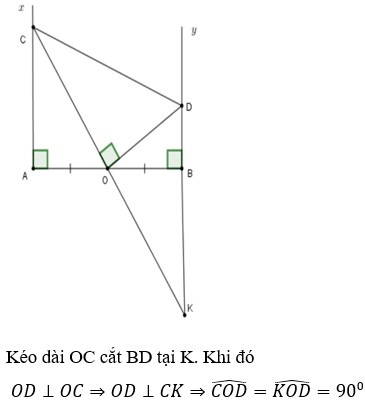
Gọi K là giao điểm của CO và BD
Xét \(\Delta\)AOC và \(\Delta\)BOK có :
AO = BO(gt)
\(\widehat{OAC}=\widehat{OBK}\left(=90^0\right)\)
\(\widehat{O}\)chung
=> \(\Delta\)AOC = \(\Delta\)BOK(g.c.g)
=> OC = OK(hai cạnh tương ứng)
AC = BK(hai cạnh tương ứng)
Xét \(\Delta\)COD và \(\Delta\)KOD có :
CO = KO(gt)
\(\widehat{OCD}=\widehat{OKD}\left(=90^0\right)\)
OD cạnh chung
=> \(\Delta\)COD = \(\Delta\)KOD(c.g.c)
=> CD = KD(hai cạnh tương ứng)
Do đó : CD = DB + BK = DB + AC

\(a)\)
Theo đề ra: \(AM=\frac{1}{3}MB\)
\(\rightarrow AM+MB=AB\)
\(\rightarrow\frac{1}{3}MB+\frac{3}{4}MB=AB\)
\(\rightarrow MA=8:4=2\)
\(MB=8-2=6\)
\(MC=\sqrt{MA^2+CA^2}=\sqrt{13}\)
\(MD=\sqrt{MB^2+BD^2}=2\sqrt{13}\)
\(CD=\sqrt{MC^2+MD^2}=\sqrt{65}\)
\(b)\)
\(MC^2+MD^2=13+52=65\)
\(CD^2=65\)
\(\rightarrow MC^2+MD^2=CD^2\)
\(\rightarrow MCD\text{ }\)\(\text{là tam giác vuông}\)