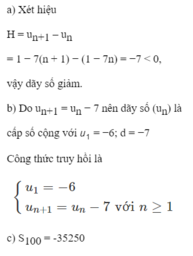Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta sử dụng công thức truy hồi để tìm các số hạng tiếp theo trong dãy:
\(1;3;2;-1;-3;-2;1;3;2;-1;-3;-2...\)
Từ đó ta nhận thấy quy luật:
\(u_n=1\) nếu \(n=6k+1\)
\(u_n=3\) nếu \(n=6k+2\)
\(u_n=2\) nếu \(n=6k+3\)
\(u_n=-1\) nếu \(n=6k+4\)
\(u_n=-3\) nếu \(n=6k+5\)
\(u_n=-2\) nếu \(n=6k\)
Đồng thời:
\(u_3=u_2-u_1\)
\(u_4=u_3-u_2\)
...
\(u_{99}=u_{98}-u_{97}\)
\(u_{100}=u_{99}-u_{98}\)
Cộng vế với vế:
\(u_3+u_4+...+u_{100}=u_{99}-u_1\)
\(\Leftrightarrow u_1+u_2+...+u_{100}=u_2+u_{99}=3+u_{6.16+3}=3+2=5\)

6:
\(u_n=8+7\left(n-1\right)=7n+1\)
7: Đặt un=7/12
=>\(\dfrac{2n+5}{5n-4}=\dfrac{7}{12}\)
=>35n-28=24n+60
=>11n=88
=>n=8
=>Đây là số hạng thứ 8
8: \(\dfrac{2n}{n^2+1}=\dfrac{9}{41}\)
=>9n^2+9=82n
=>9n^2-82n+9=0
=>(9n-1)(n-9)=0
=>n=9(nhận) hoặc n=1/9(loại)
=>Đây là số thứ 9
10B
9D

Câu 1:
Dãy đã cho có thể viết dưới dạng công thức truy hồi sau:
\(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=u_n+7n\end{matrix}\right.\)
\(u_{n+1}=u_n+7n\Leftrightarrow u_{n+1}-\dfrac{7}{2}\left(n+1\right)^2+\dfrac{7}{2}\left(n+1\right)=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\)
Đặt \(v_n=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\Rightarrow\left\{{}\begin{matrix}v_1=1\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=1\)
\(\Rightarrow u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n=1\)
\(\Leftrightarrow u_n=\dfrac{7}{2}n^2-\dfrac{7}{2}n+1\)
\(\dfrac{7}{2}n^2-\dfrac{7}{2}n+1=35351\)
\(\Leftrightarrow\dfrac{7}{2}n^2-\dfrac{7}{2}n-35350=0\)
\(\Rightarrow n=101\)
Vậy đó là số hạng thứ 101
2.
Do a;b;c lập thành 1 cấp số cộng
\(\Rightarrow a+c=2b\)
\(\Leftrightarrow2R.sinA+2R.sinC=2.2R.sinB\)
\(\Leftrightarrow sinA+sinC=2sinB\)
\(\Leftrightarrow2sin\dfrac{A+C}{2}.cos\dfrac{A-C}{2}=4sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{B}{2}cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}=2cos\dfrac{A+C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)+sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)=2cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)-2sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right).cos\left(\dfrac{C}{2}\right)=3sin\left(\dfrac{A}{2}\right).sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cot\left(\dfrac{A}{2}\right).cot\left(\dfrac{C}{2}\right)=3\)

Chọn C
Theo đề bài ta có:
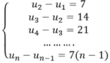
Cộng vế với vế các phương trình của hệ ta được:
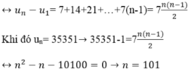

Theo đầu bài ta có :
\(\begin{cases}u_2-u_1=7\\u_3-u_2=14\\u_4-u_3=21.......\\....u_n-u_{n-1}=7\left(n-1\right)\end{cases}\)
Cộng các vế của các phương trình của hệ, ta được :
\(\Leftrightarrow u_n-u_1=7+14+21+.....+7\left(n-1\right)=7\frac{n\left(n-1\right)}{2}\left(1\right)\)
Đặt \(u_n=35351\Rightarrow\left(1\right)\Leftrightarrow35351-1=7\frac{n\left(n-1\right)}{2}\)
\(\Leftrightarrow n^2-n-10100=0\rightarrow n=101\)
Do đó 35351 là số hạng thứ 101 của dãy số

Gọi cấp số nhân tăng nghiêm ngặt là \(a_n\). Theo đầu bài ta có \(a_2,a_4\) là 2 nghiệm của phương trình
\(t^2-30t+144=0\Leftrightarrow\begin{cases}t=6\\t=24\end{cases}\)
\(\Leftrightarrow\begin{cases}a_2=6\\a_4=24\end{cases}\) hoặc \(\begin{cases}a_2=24\\a_4=6\end{cases}\)
\(\Leftrightarrow\begin{cases}a_1q=6\\a_1q^3=24\end{cases}\) hoặc \(\begin{cases}a_1q=24\\a_1q^3=6\end{cases}\)
\(\Leftrightarrow\begin{cases}a_1q=6\\q^2=4\end{cases}\) hoặc \(\begin{cases}a_1q=24\\q^2=\frac{6}{24}=\frac{1}{4}\end{cases}\)
\(\Leftrightarrow\begin{cases}a_1=\frac{6}{\pm2}\\q=\pm2\end{cases}\) hoặc \(\begin{cases}a_1=24\left(\pm2\right)\\q=\pm\frac{1}{2}\end{cases}\)
Do cấp số nhân tăng nghiêm ngặt, nên q>1, do vậy ta chọn \(a_1=3;q=2\)
Cho nên \(S_{10}=u_1\frac{2^{10}-1}{2-1}=3.\left(1024-1\right)=3069\)
Giao lưu:
Gọi dãy số đã co có dạng: \(U_1;U_2;U_3;U_4;U_5...U_{10}...U_n\)
đầu bài ta có hệ phương trình.
\(\left\{\begin{matrix}U_n.q=U_{\left(n+1\right)}\left(1\right)\\q>1\left(2\right)\\U_2+U_4=144\left(3\right)\\U_2.U_4=30\left(4\right)\end{matrix}\right.\)
Thế (3) vào (4) \(\Leftrightarrow U_2\left(144-U_2\right)=30\Leftrightarrow U_2^2-144U_4+30=0\Rightarrow\left[\begin{matrix}U_2=24\\U_2=6\end{matrix}\right.\)
Vì U2 và U4 có vai trò như nhau
do vậy có cắp nghiệm là hoán đổi (U2,U4)=(6,24)(*)
Từ (1) và (2) ta có(*)=> \(\left\{\begin{matrix}U_2=6\\U_4=24\end{matrix}\right.\)(**)
Từ (1) ta có: \(U_4=q.U_3=q.\left(q.U_2\right)=q^2.U_2\)(4)
Từ (**) và (4) ta có \(\frac{U_4}{U_2}=q^2=\frac{24}{6}=4\Rightarrow!q!=2\) (5)
Từ (3) và (5) => q=2
Vậy tổng 10 số hạng đầu tiên của dẫy là :\(S_{10}=2^0.3+2^1.3+3.2^2+...+3.2^8+3.2^9=3.\left(1+2+2^2+..+2^9\right)\)
\(S_{10}=3.\left(2^{10}-1\right)\)