Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(P(x) = 4{x^2} + 1 + 3x = 4{x^2} + 3x + 1\) ; \(Q(x) = 5x + 2{x^2} + 3 = 2{x^2} + 5x + 3\).
b)
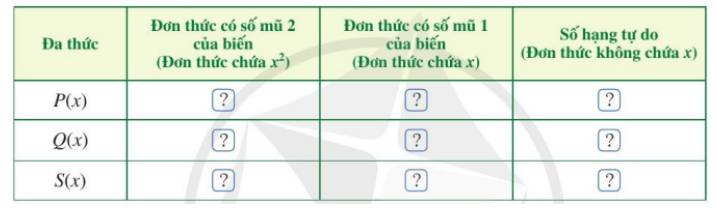
Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa \({x^2}\)) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
P(x) | \(4{x^2}\) | 3x | 1 |
Q(x) | \(2{x^2}\) | 5x | 3 |
S(x) | \(2{x^2}\) | – 2x | – 2 |
c) Vậy \(S(x) = 2{x^2} - 2x - 2\)

a) Sắp xếp đa thức (một biến) theo số mũ giảm dần của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần của biến.
b) Quan sát bảng để đưa ra các đơn thức thích hợp phù hợp với biến có số mũ tương ứng.
c) Xác định đơn thức R(x) dựa vào kết quả phần b).
Lời giải chi tiết:
a) \(P(x) = 5{x^2} + 4 + 2x = 5{x^2} + 2x + 4\); \(Q(x) = 8x + {x^2} + 1 = {x^2} + 8x + 1\).
b)
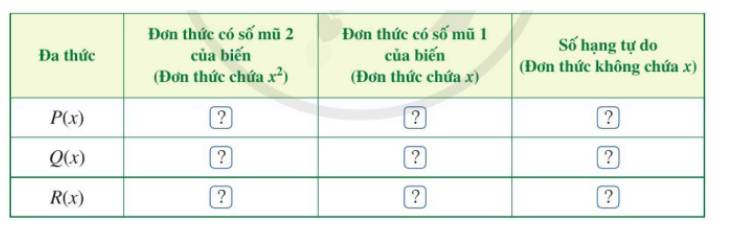
Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa \({x^2}\)) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
P(x) | \(5{x^2}\) | 2x | 4 |
Q(x) | \({x^2}\) | 8x | 1 |
R(x) | \(6{x^2}\) | 10x | 5 |
c) Vậy \(R(x) = 6{x^2} + 10x + 5\).

a) P(x) = \(7 + 4{x^2} + 3{x^3} - 6x + 4{x^3} - 5{x^2}\)
\( = 7{x^3} - {x^2} - 6x + 7\)
b) Đa thức P(x) có bậc là 3
Hệ số cao nhất là 7
Hệ số của \({x^2}\)là -1
Hệ số của \(x\)là -6
Hệ số tự do là 7

a)
P(x) = x3 + 4x3 +3x - 6x - 4 - x2
P(x) = 5x3 -x2 -3x-4
Hệ số cao nhất là: 5
Hẹ số tự do là: -4
Q(x)= -x3 -x3 + 3x+8
Q(x) = -2x2 + 3x+8
\(P\left(x\right)=x^3+4x^3+3x-6x-4-x^2\)
\(P\left(x\right)=\left(x^3+4x^3\right)-x^2+\left(3x-6x\right)-4\)
\(P\left(x\right)=5x^3-x^3-3x-4\)
\(\text{Hệ số cao nhất:5}\)
\(\text{Hệ số tự do:-4}\)
\(Q\left(x\right)=-x^3-x^3+3x+8\)
\(Q\left(x\right)=\left(-x^3-x^3\right)+3x+8\)
\(Q\left(x\right)=-2x^3+3x+8\)

a) \(P\left(x\right)=3x^3-2x+2x^2+7x+8-x^4)\)
\(P\left(x\right)=3x^3(-2x+7x)+2x^2+8-x^4)\)
\(P\left(x\right)=3x^3+5x+2x^2+8-x^4)\)
\(P\left(x\right)=-x^4+3x^3+2x^2+5x+8\)
\(Q\left(x\right)=2x^2-3x^3+3x^2-5x^4\)
\(Q\left(x\right)=(2x^2+3x^2)-3x^3-5x^4\)
\(Q\left(x\right)=5x^2-3x^3-5x^4\)
\(Q\left(x\right)=-5x^4-3x^2+5x^2\)
b)
\(P\left(x\right)+Q\left(x\right)=(3x^3-2x+2x^2+7x+8-x^4)+\left(2x^2-3x^3+3x^2-5x^4\right)\)
\(P\left(x\right)+Q\left(x\right)=3x^3-2x+2x^2+7x+8-x^4+2x^2-3x^3+3x^2-5x^4\)
\(P\left(x\right)+Q\left(x\right)=\left(3x^3-3x^3\right)+\left(-2x+7x\right)+\left(2x^2+2x^2+3x^2\right)+8+\left(-x^4-5x^4\right)\)\(P\left(x\right)+Q\left(x\right)=5x+7x^2+8-6x^4\)
Vậy: \(R\left(x\right)\) \(=5x+7x^2+8-6x^4\)
c. \(R\left(x\right)\) \(=5x+7x^2+8-6x^4\)
\(=5x+7x^2+4+4-6x^4\)
\(=\) \((12x-4)^2+4\ge4-6x^4\)
Câu c MIK KHÔNG CHẮC LÀ ĐÚNG

a) \(\begin{array}{l}P(x) = {x^2}({x^2} + x + 1) - 3x(x - a) + \dfrac{1}{4} = {x^4} + {x^3} + {x^2} - 3{x^2} + 3ax + \dfrac{1}{4}\\ = {x^4} + {x^3} - 2{x^2} + 3ax + \dfrac{1}{4}\end{array}\).
b) Các hệ số có trong đa thức P(x) là: 1; 1; – 2; 3a; \(\dfrac{1}{4}\).
Tổng các hệ số bằng \(\dfrac{5}{2}\)hay:
\(\begin{array}{l}1 + 1 - 2 + 3a + \dfrac{1}{4} = \dfrac{5}{2}\\ \to 3a = \dfrac{9}{4}\\ \to a = \dfrac{3}{4}\end{array}\)
Vậy \(a = \dfrac{3}{4}\).

\(P(x) =7 + 10{x^2} + 3{x^3} - 5x + 8{x^3} - 3{x^2}\\=(3{x^3}+8{x^3})+( 10{x^2} - 3{x^2})-5x + 7\\= 11{x^3} + 7{x^2} - 5x + 7\)
a) \(R(x) = - 2{x^2} + 3{x^2} + 6x + 8{x^4} - 1 = ( - 2{x^2} + 3{x^2}) + 6x + 8{x^4} - 1 = {x^2} + 6x + 8{x^4} - 1\).
b) Trong các đơn thức của đa thức R(x) ta thấy, số mũ lớn nhất là 4, sau đó đến 2; 1 và 0.
Vậy \(R(x) = {x^2} + 6x + 8{x^4} - 1 = 8{x^4} + {x^2} + 6x - 1\).