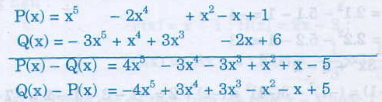Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

P (x) = x5 + 2x4 + x2 - x +1
Q (x) = 6 - 2x + 3x3 + x4 - 3x5
P (x) - Q (x) = (x5 + 2x4 + x2 - x +1) - ( 6 - 2x + 3x3 + x4 - 3x5)
= x5 + 2x4 + x2 - x +1 - 6 + 2x - 3x3 - x4 + 3x5
= ( x5 + 3x5 ) + ( 2x4 - x4 ) - 3x3 + x2 + ( -x + 2x ) +( 1 - 6 )
= 4x5 + x4 - 3x3 + x2 + x - 5
Q (x) - P (x) = ( 6 - 2x + 3x3 + x4 - 3x5 ) - (x5 + 2x4 + x2 - x +1)
= 6 - 2x + 3x3 + x4 - 3x5 - x5 - 2x4 - x2 + x -1
= - ( 3x5 + x5 ) + ( x4 - 2x4 ) + 3x3 - x2 - ( 2x - x ) + ( 6 - 1)
= - 4x5 - x4 + 3x3 - x2 - x + 5
* Nhận xét: Hệ số của hai đa thức P (x) và Q(x) đối nhau.

Vì đa thức g(x) là đa thức bậc 3 và mọi nghiệm của f(x) cũng là của g(x) nên:
G/s \(g\left(x\right)=\left(x-1\right)\left(x+3\right)\left(x-c\right)\) \(\left(c\inℝ\right)\)
Khi đó: \(x^3-ax^2+bx-3=\left(x-1\right)\left(x+3\right)\left(x-c\right)\)
\(\Leftrightarrow x^3-ax^2+bx-3=\left(x^2+2x-3\right)\left(x-c\right)\)
\(\Leftrightarrow x^3-ax^2+bx-3=x^3-\left(c-2\right)x^2-\left(2c+3\right)x+3c\)
Đồng nhất hệ số ta được:
\(\hept{\begin{cases}a=c-2\\b=-2c-3\\c=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-3\\b=-1\\c=-1\end{cases}}\)
Vậy a = -3 , b = -1

(x-1) x f(x)=(x+2) x f(x+3)
Thay x=1 : (1-1) x f(1) = (1+2) x f(1+3)
=>f(4)=0
Thay x=-2 :(-2-1) x f(-2) = (-2+2) x f(-2+3)
=>f(-2)=0
Thay x=4(thay bang 0 vi f(4)=0).....
Thay x=7 (ket qua o tren)
Thay x=10 kq o tren
vay 5 nghiem la 1;2;4;7;10
mk chi tom tat thoi nha chuc bn hoc tot

Ta có: Với 1=0 thì (1-1).f(1)=(1+2).f(1+3) hay 0=3.f(4) do 3 khác 0 nên f(4)=0 vậy 4 là 1 nghiệm của f(x)
Với x=-2 thì (-2-1).f(-2)=(-2+2).f(-2+3) hay (-3).f(-2)=0 do -3 khác 0 nên f(-2)=0 vậy -2 là 1 nghiệm của f(x)
Với x=4 ta có: (4-1).f(4)=(4+2).f(4+3) suy ra 0=6.f(7) (vì f(4)=0)
do 6 khác 0 nên f(7)=0 hay 7 là 1 nghiệm của f(x)
Với x=7 ta có: (7-1).f(7)=(7+2).f(7+3) suy ra 0=9.f(10) (vì f(7)=0)
do 9 khác 0 nên f(10) bằng 0 hay 10 là 1 nghiệm của f(x)
Với x=10 ta có: (10-1).f(10)=(10+2).f(10+3) suy ra 0=12.f(13) (vì f(10)=0)
do 12 khác 0 nên f(13)=0 hay 13 là 1 nghiệm của f(x)
Vậy 5 nghiệm của f(x) tìm được là: -2;4;7;10;13
Không chứng minh tương tự được hả bạn???
Tại sao lại với 1=0?

\(M\left(x\right)+N\left(x\right)\)
\(=5x^3-x^2-4+2x^4-2x^2+2x+1\)
\(=2x^4+5x^3-3x^2+2x-3\)
\(M\left(x\right)-N\left(x\right)\)
\(=5x^3-x^2-4-\left(2x^4-2x^2+2x+1\right)\)
\(=5x^3-x^2-4-2x^4+2x^2-2x-1\)
\(=-2x^4+5x^3+x^2-2x-5\)
\(M\left(x\right)+P\left(x\right)=N\left(x\right)\)
\(\Rightarrow P\left(x\right)=N\left(x\right)-M\left(x\right)\)
\(\Rightarrow P\left(x\right)=2x^4-2x^2+2x+1-\left(5x^3-x^2-4\right)\)
\(\Rightarrow P\left(x\right)=2x^4-2x^2+2x+1-5x^3+x^2+4\)
\(\Rightarrow P\left(x\right)=2x^4-5x^3-x^2+2x+5\)