Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mọi người giúp mình với!!!!!!!!!!!!!!!!!!
cảm ơn mọi người
b) \(x^4+2x^2+1=0\)
\(\Rightarrow\left(x^2+1\right)^2=0\)
Mà: \(\left(x^2+1\right)^2>0\)
=> P(x) ko có nghiệm
c) \(16x^2y^5-2x^3y^2=\dfrac{15}{4}\)

\(a)\) Ta có :
\(A=\frac{1}{x^2-4x+7}\)
\(A=\frac{1}{\left(x^2-4x+4\right)+3}\)
\(A=\frac{1}{\left(x-2\right)^2+3}\)
Lại có :
\(\left(x-2\right)^2\ge0\)
\(\Rightarrow\)\(\left(x-2\right)^2+3\ge3\)
\(\Rightarrow\)\(A=\frac{1}{\left(x-2\right)^2+3}\le\frac{1}{3}\)
Dấu "=" xảy ra khi và chỉ khi \(\left(x-2\right)^2+3=3\)
\(\Leftrightarrow\)\(\left(x-2\right)^2=3-3\)
\(\Leftrightarrow\)\(\left(x-2\right)^2=0\)
\(\Leftrightarrow\)\(x-2=0\)
\(\Leftrightarrow\)\(x=2\)
Vậy GTLN của \(A\) là \(\frac{1}{3}\) khi 2\(x=2\)
Chúc bạn học tốt ~
\(b)\) Ta có :
\(f\left(x\right)=x^2-4x+7\)
\(f\left(x\right)=\left(x^2-4x+4\right)+3\)
\(f\left(x\right)=\left(x-2\right)^2+3\ge3>0\)
Vậy đa thức \(f\left(x\right)\) vô nghiệm
Chúc bạn học tốt ~

a: f(2)=2*2^2-3*2+4=8-6+4=2+4=6
b: h(x)=-2x^2+x-1+f(x)
=-2x^2+x-1+2x^2-3x+4
=-2x+3

a, Thay x = -2 ; y = 3 ta được
\(A=\dfrac{4\left(-2\right)-5.3}{8\left(-2\right)-7.3}=\dfrac{-8-15}{-16-21}=\dfrac{23}{37}\)
b, Ta có \(\dfrac{x}{y}=\dfrac{5}{4}\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=k\Rightarrow x=5k;y=4k\)
Thay vào ta được \(A=\dfrac{4.5k-5.4k}{8.5k-7.4k}=\dfrac{0}{40k-28k}=0\)

Bài 1:
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=1\\2a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-2\end{matrix}\right.\)

ta có x = -1
mà x có lũy thừa bậc chẵn nên A = 1 + 1 + ... + 1 = 50
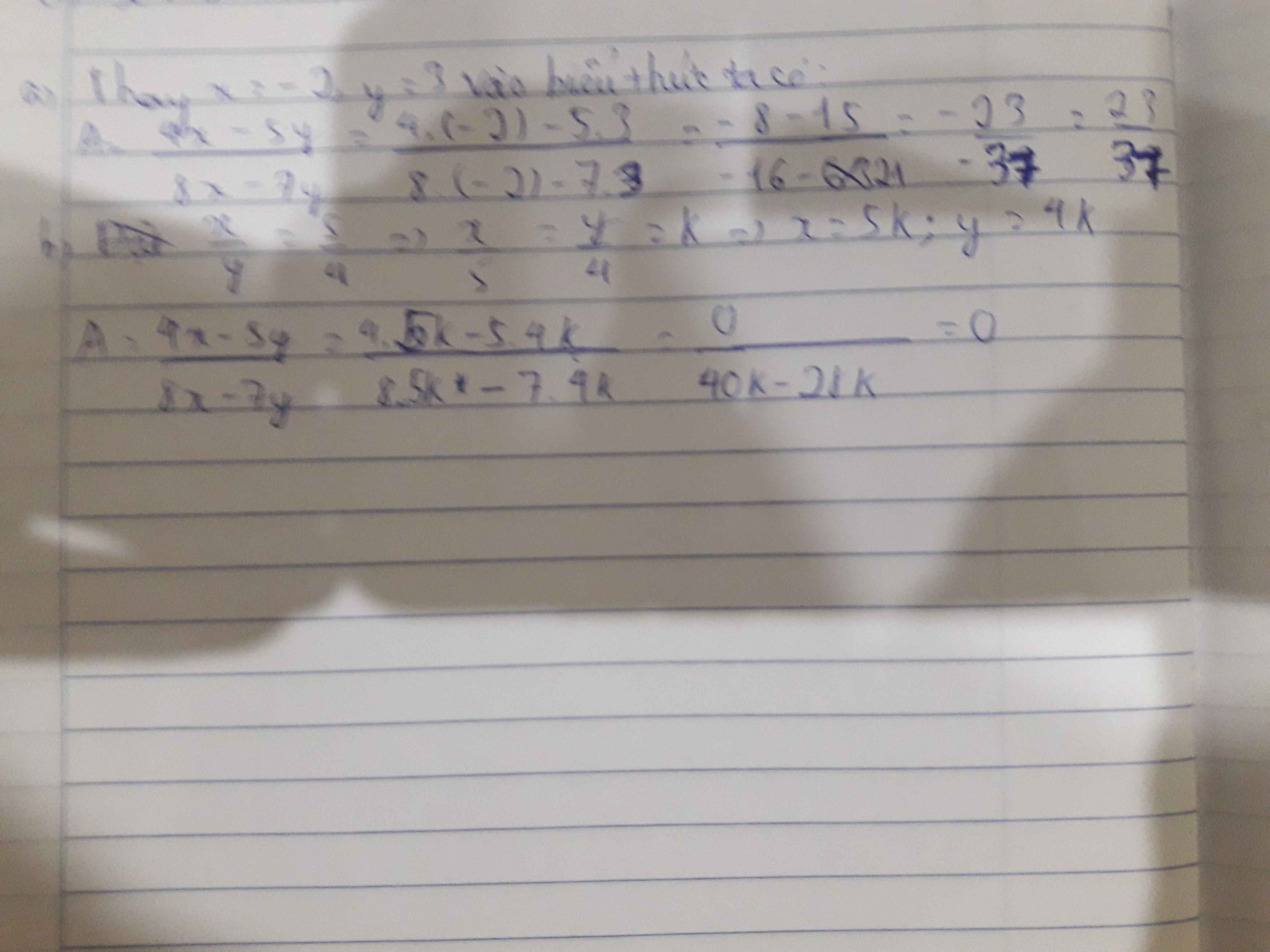
Đề sai rồi bạn
Sửa đề: f(x) = x² - 4x + 3
a) f(0) = 0 - 4.0 + 3 = 3
f(1) = 1 - 4.1 + 3 = 0
f(3) = 9 - 4.3 + 3 = 0
b) x = 1 và x = 3 là nghiệm của đa thức f(x) vì f(1) = 0 và f(3) = 0