Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có:
(1)
(3)
(số đo góc nội tiếp bằng nửa số đo của cung bị chắn).
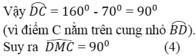
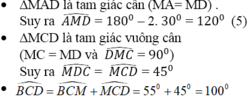
(theo (2) và (6) và Cm là tia nằm giữa hai tia CB,CD).
a) Xét (O) có :
AB là tiếp tuyến tại B
AC là tiếp tuyến tại C
AB cắt AC tại A
\(\Rightarrow\widehat{ABO}=\widehat{ACO}=90^o\)và OA là p/g \(\widehat{BOC}\)
Xét tg ABOC có \(\widehat{ABO}+\widehat{ACO}=180^o\)Mà 2 góc này đối nhau
\(\Rightarrow\)ABOC là tg nt
b) Xét (O) có
\(\widehat{ABE}\)là góc tạo bởi tiếp tuyến AB và dây BE
\(\widehat{BDE}\)là góc nt chắn cung BE
\(\Rightarrow\widehat{ABE}=\widehat{BDE}=\frac{1}{2}sđ\widebat{BE}\)
Xét \(\Delta ABEvà\Delta ADB:\)
\(\widehat{BAD}\)chung
\(\widehat{ABE}=\widehat{BDE}\)
\(\Rightarrow\Delta ABE\infty\Delta ADB\left(gg\right)\)
\(\Rightarrow\frac{AB}{AD}=\frac{AE}{AB}\Rightarrow AB^2=AD.AE\)
c) Vì OA là p/g \(\widehat{BOC}\Rightarrow\widehat{BOA}=\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Do ABOC là tg nt\(\Rightarrow\widehat{BOA}=\widehat{BCA}\)(cùng chắn cung AB)
Suy ra \(\widehat{AOC}=\widehat{ACB}\)
A B C D M
Đây là hình với cả đã chứng minh được Cm là phân giác góc BCD,bn nào giúp mik với nhé ^^~
M A B C I D N O H K
a) CM: \(\widehat{OBM}=\widehat{ODC}\)
\(\widehat{OBM}+\widehat{OBC}=180^o\)( kề bù)
\(\widehat{ODC}+\widehat{OBC}=180^o\)( tứ giác ODCB nội tiếp )
=> \(\widehat{OBM}=\widehat{ODC}\)
b)
+)Xét tam giác MCN có CO là tia phân giác đồng thời là đường cao
=> Tam giác CMN cân tại C (1)
=> \(\widehat{BMA}=\widehat{DNA}=\widehat{BAM}\)( CD//BA => DN//BA)
=> Tam giác BMA cân tại B
=> BM=BA=CD ( ABCD là hình bình hành) (2)
+) CO là phân giác \(\widehat{BCD}\)
=> \(\widebat{BO}=\widebat{DO}\)
=> BO=DO (3)
+) Xét tam giác BOM và tam giác DOC có:
\(\widehat{OBM}=\widehat{ODC}\)( theo a)
BM=CD ( theo 2)
BO=DO (theo 3)
=> \(\Delta BOM=\Delta DOC\)
+) OM=OC
Và từ (1) => CO là đường trung trực của MN
=> OM=ON
Vậy OM=ON=OC
=> O là tâm đường tròn ngoại tiếp tam giác CMN
c) GỌi H là giao của IO và BD
=> IH vuông BD và H là trung điể m BD
Ta có: \(KD^2=\left(HD-HK\right)^2=HD^2+HK^2-2.HD.HK=ID^2-IH^2+IK^2-IH^2-2HD\left(HD-KD\right)\)
\(=ID^2+IK^2-2\left(IH^2+HD^2\right)+2HD.KD=ID^2+IK^2-2ID^2+2HD.KD\)
\(=IK^2-ID^2+2HD.KD\)
=> \(IB^2-IK^2=ID^2-IK^2=2HD.KD-KD^2\)
=> \(\frac{IB^2-IK^2}{KD^2}=\frac{2HD-KD}{KD}=\frac{BD-KD}{KD}=\frac{BK}{KD}\)(4)
Ta lại có: CK là phân giác trong của tam giác CBD
=> \(\frac{BK}{KD}=\frac{CB}{CD}\)
Và MB=DC ( theo cm câu a) , CM=CN ( Tam giác CMN cân)
=> CB=DN
=> \(\frac{BK}{KD}=\frac{DN}{MB}\)(5)
Từ (4), (5)
=> ĐPCM
a . Gọi O là tâm của đường tròn có đường kính BC.
Xét \(\Delta\)BMC vuông tại M có O là trung điểm của BC (OB=OC)
\(\Rightarrow CB=MO=OC\)
\(\Leftrightarrow M\in\left(O;OB\right)\left(1\right)\)
Xét hình thang ABCD có :
M là trung điểm của AD;O là trung điểm của BC
\(\Rightarrow MO\) là đường trung bình
\(\Leftrightarrow\)AB//MO
Mà AD\(\perp\)AB
\(\Rightarrow MO\perp AD\left(2\right)\)
Từ \(\left(1\right)\left(2\right)suyra\) AD là tiếp tuyến của đường tròn đường kính BC
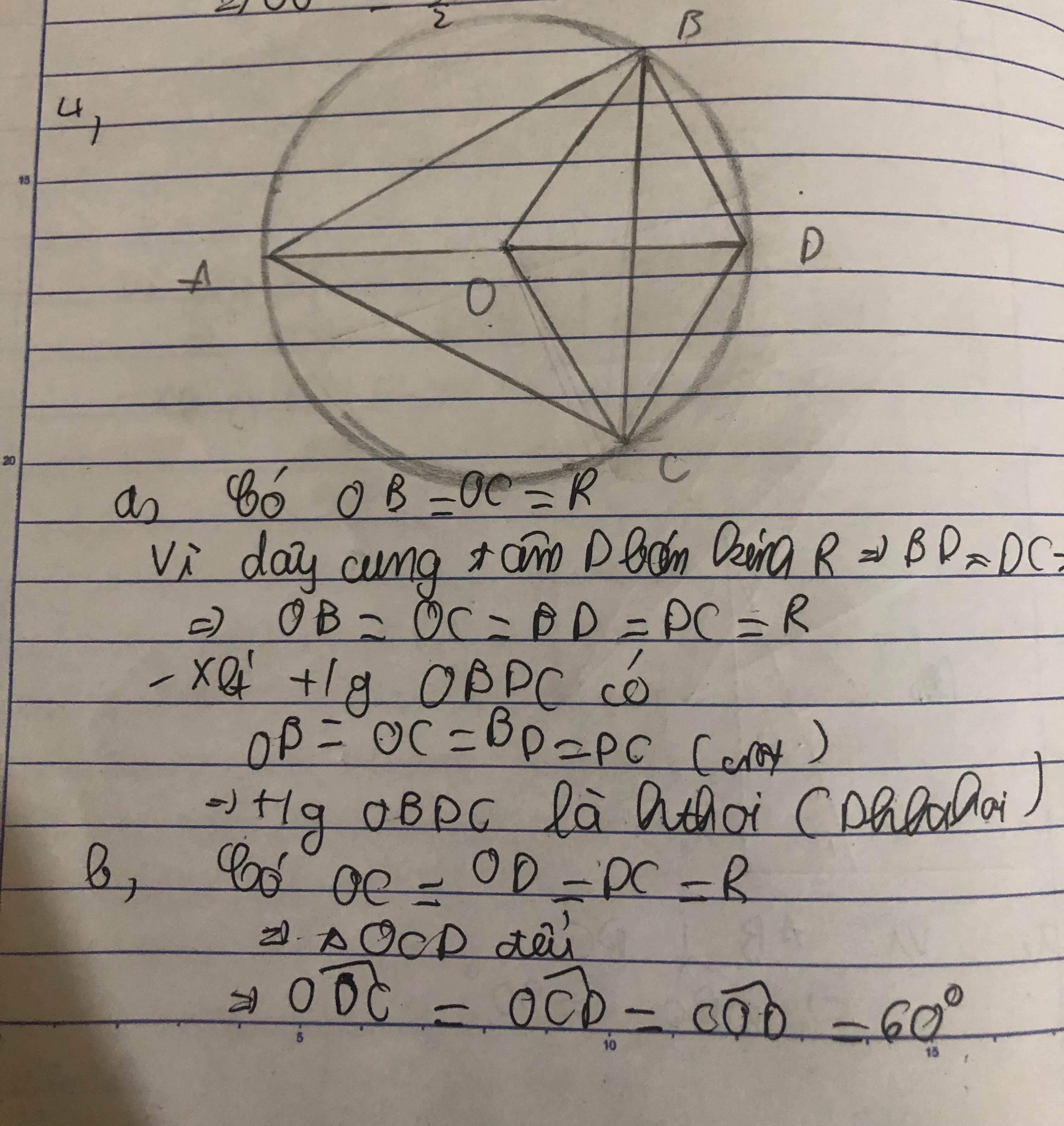
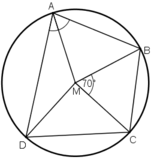
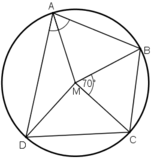
Ta có:
= 
- 
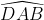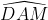= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên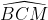
= 
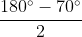= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên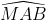
= 50o (theo (1))
Vậy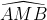
= 180o – 2. 50o = 80o
=> sđ cung BCD = 2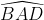
= 2. 80o = 160o
Mà sđ cung BC =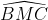
= 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra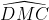
= 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra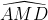
= 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và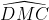
= 90o
Suy ra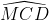
= 
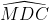= 45o (6)
Ta có: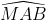
= 
- 
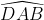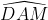= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên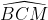
= 
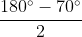= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên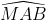
= 50o (theo (1))
Vậy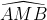
= 180o – 2. 50o = 80o
=> sđ cung BCD = 2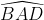
= 2. 80o = 160o
Mà sđ cung BC =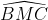
= 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra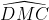
= 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra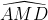
= 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và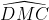
= 90o
Suy ra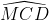
= 
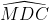= 45o (6)