cho a= 5/n+3 tìm n đểa A là 1 phân sốb a là 1 số tự nhiên2 cho b =3n-5/n+4 tìm n đểa A l...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

TT

Trần Thanh Vân

18 tháng 8 2021

cho a= 5/n+3 tìm n để

a A là 1 phân số

b a là 1 số tự nhiên

2 cho b =3n-5/n+4 tìm n để

a A là 1 phân số

b a là 1 số tự nhiên

4

TC

Trên con đường thành công không có....

18 tháng 8 2021

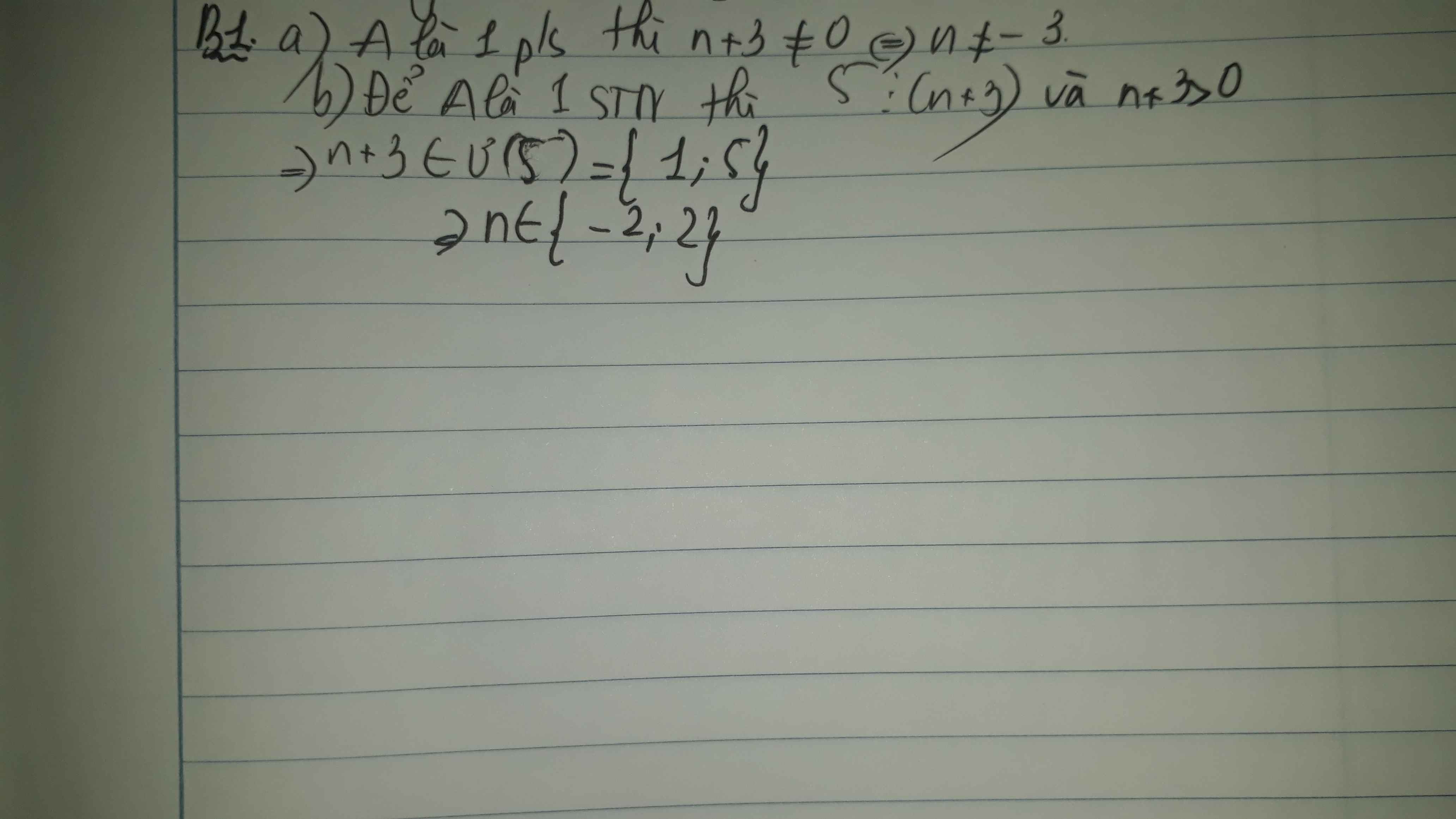
undefined

TC

Trên con đường thành công không có....

18 tháng 8 2021

undefined

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

phạm thị diễm quỳnh

9 tháng 4 2015 - olm

cho biểu thức A=(2n+1)/(n-3) + (3n-5) /(n-3) - (4n-5) / (n-3)

a)Rút gọn A

b)tìm số tự nhiên n để A nhận giá trị là số nguyên

c)tìm số nguyên n để phân số A sau khi rút gọn là phân số tối giản

0

CY

Cao yến Chi

14 tháng 4 2020 - olm

bài 1: với mọi số tự nhiên n chứng minh các phân số sau là phân số tối giản

A=2n+1/2n+2

B=2n+3/3n+5

Bài 2:

a) Cho phân số: N=5n+7/2n+1( n thuộc Z, n khác -1/2). Tìm n để N là phân số tối giản

b) Cho phân số: P=5-2n/4n+5 ( n thuộc Z, n khác -5/4). Tìm n để P là phân số tối giản

giúp mk với

mk sẽ tick cho!!

6

NP

Nguyễn Phương Uyên

14 tháng 4 2020

b1 :

a, gọi d là ƯC(2n + 1;2n +2)

=> 2n + 1 chia hết cho d và 2n + 2 chia hết cho d

=> 2n + 2 - 2n - 1 chia hết cho d

=> 1 chia hết cho d

=> d = 1

=> 2n+1/2n+2 là ps tối giản

NT

Nguyễn Thị Huyền Trang

14 tháng 4 2020

Bài 1: Với mọi số tự nhiên n, chứng minh các phân số sau là phân số tối giản:

A=2n+1/2n+2

Gọi ƯCLN của chúng là a

Ta có:2n+1 chia hết cho a

2n+2 chia hết cho a

- 2n+2 - 2n+1

- 1 chia hết cho a

- a= 1

Vậy 2n+1/2n+2 là phân số tối giản

B=2n+3/3n+5

Gọi ƯCLN của chúng là a

2n+3 chia hết cho a

3n+5 chia hết cho a

Suy ra 6n+9 chia hết cho a

6n+10 chia hết cho a

6n+10-6n+9

1 chia hết cho a

Vậy 2n+3/3n+5 là phân số tối giản

Mình chỉ biết thế thôi!

#hok_tot#

L

linhnhiiii

2 tháng 5 2016 - olm

Cho A =5/n—1

A) tìm điều kiện của n để A là phân số

B) tìm n thuộc z để A thuộc z

C) tìm số tự nhiên n để A đạt số tự nhiên

0

S

ßØ§§™

27 tháng 2 2019 - olm

1. Tìm tất cả các phân số = phân số 34/51 và có mẫu là số tự nhiên ngỏ hơn 16

2. Cho A= 5/n-4

a, Tìm n thuộc Z để A là phân số

b, tìm n thuộc z để a là số nguyên

3. Cho B=x-2/x+51

a, tìm x thuộc z để b là phân số

b, tìm x thuộc z để b là số nguyên

0

PT

Phạm Thanh Ngọc

14 tháng 11 2021 - olm

Bài 1. Tìm số tự nhiên a nhỏ nhất để a : 7 dư 4; a : 9 dư 5 và a : 15 dư 8.

Bài 2. a) Tìm số tự nhiên n để 16 – 3n là ước của 2n + 1.

b) Tìm số tự nhiên n để n2 + 6n là số nguyên tố.

Bài 3. a) Tìm số nguyên tố p sao cho p + 2; p + 6; p + 8; p + 12; p + 14 cũng là số nguyên tố

b) Tìm số tự nhiên n để các số sau nguyên tố cùng nhau: 4n – 3 và 6n + 1

0

NQ

Nguyễn Quốc Tuấn

2 tháng 4 2020 - olm

Cho biểu thức A=10/(n+1)(n-2),n thuộc Za,Tìm điều kiện để A là phân sốb,Với giá trị n bằng bao nhiêu thì phân số A không tồn tại?c,Tính A biết n=0;n=1;n=2 Tím số tự nhiên n để phân số 6n+99/3n+4 Tìm giá trị nguyên của n để phân số A=3n+2/n-1 là số nguyên Cho biểu thức C=x-3/x-6,x thuộc Za,Tìm số nguyên x để C là phân sốb,Tìm các số nguyên x để C là số nguyên...

0

HQ

Hồ Quỳnh Giang

20 tháng 2 2020 - olm

Câu a,Cho biểu thức A= -5/n-21, tìm các số tự nhiên n để biểu thức A là phân số.2, tìm các số tự nhiên n để biểu thức A là số nguyênCâu b,Tìm giá trị nguyên của n để phân số A=3n+2/n-1có giá trị là số nguyênCâu c, tìm các giá trị nguyên n để phân số A=4n+5/2n-1 có giá trị là số nguyên Mng giải giúp mik vs...

0

YN

Yến Nhi Libra Virgo HotGirl Sakura

5 tháng 4 2017 - olm

Câu 3 : Cho phân số \(P=\frac{n+4}{2n-1}\)với n là số tự nhiên

a. Tìm số tự nhiên n để phân số P không tối giản

b. Tìm số tự nhiên n để phân số P là số nguyên tố

Câu 4 : Tìm số có hai chữ số ab sao cho ab = a + b²

1

DP

Đức Phạm

6 tháng 4 2017

Câu 3 :

b. P là nguyên tố khi và chỉ khi n + 4 chia hết cho 2n - 1

=> 2n + 8 chia hết cho 2n - 1

mà 2n - 1 chia hết cho 2n - 1 . Suy ra 9 chia hết cho 2n - 1

=> 2n - 1 \(\inƯ\)(9) = { 1 , 3 , 9 }

=> 2n - 1 \(\in\) { 1 ,3 , 9 }

=> 2n\(\in\){ 2 , 4 ,10}

=> n\(\in\){ 1, 2 ,5 }

=> P\(\in\){ 5 , 2 , 1 }

Vì P là nguyên tố nên P\(\in\){ 5,2}

vậy n\(\in\){ 1 , 2 }

Câu 4 :

NT

Nguyễn Thị Thu Thảo

16 tháng 2 2017 - olm

a)Tìm số nguyên n sao cho (3n-4) chia hết cho (1-2n)

b)Tìm số tự nhiên n<10 để n^2+3 /n-1 là phân số tối giản

0