
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
Biểu diễn tập A,B trên trục số bạn sẽ thấy để $A\cap B$ nhận 1 giá trị duy nhất khi:
\(\left[\begin{matrix} m^2+1=3m-1\\ -3=4(\text{vô lý})\end{matrix}\right.\Rightarrow m^2-3m+2=0\Leftrightarrow (m-1)(m-2)=0\)
\(\Rightarrow \left[\begin{matrix} m=1\\ m=2\end{matrix}\right.\)
Thử lại thấy $m=2$ không thỏa mãn vì khi đó $3m-1>4$
Vậy có 1 giá trị nguyên của $m$ thỏa mãn
Đáp án C
Lời giải:
Biểu diễn tập A,B trên trục số bạn sẽ thấy để $A\cap B$ nhận 1 giá trị duy nhất khi:
\(\left[\begin{matrix} m^2+1=3m-1\\ -3=4(\text{vô lý})\end{matrix}\right.\Rightarrow m^2-3m+2=0\Leftrightarrow (m-1)(m-2)=0\)
\(\Rightarrow \left[\begin{matrix} m=1\\ m=2\end{matrix}\right.\)
Thử lại thấy $m=2$ không thỏa mãn vì khi đó $3m-1>4$
Vậy có 1 giá trị nguyên của $m$ thỏa mãn
Đáp án C

a: Để A giao B là rỗng thì \(m< 3m+3\)
\(\Leftrightarrow-2m< 3\)
hay \(m>-\dfrac{3}{2}\)
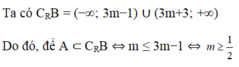
Điều kiện tồn tại của A là: 3m-1<3m+7 <=> -1<7 (luôn đúng)
Để A giao B = \(\varnothing\)
\(\Leftrightarrow\orbr{\begin{cases}3m+7\le-1\\3m-1\ge1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}m\le\frac{-8}{3}\\m\ge\frac{2}{3}\end{cases}}\)
Vậy \(m\in(-\infty;\frac{-8}{3}]U[\frac{2}{3};+\infty)\)