Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(F=k\frac{\left|q_1q_2\right|}{r^2}=9.10^9\frac{\left|4.10^{-7}.4.10^{-7}\right|}{0,05^2}=0,576\left(N\right)\)
b)
b1: Tác dụng của q1 lên q3: \(F_{13}=k\frac{\left|q_1q_2\right|}{r^2}=9.10^9\frac{\left|4.10^{-7}.-4.10^{-7}\right|}{0,03^2}=1,6\left(N\right)\)
Tác dụng của q2 lên q3: \(F_{23}=k\frac{\left|q_1q_2\right|}{r^2}=9.10^9\frac{\left|4.10^{-7}.-4.10^{-7}\right|}{0,02^2}=3,6\left(N\right)\)
Vì F13 Cùng phương, cùng chiều với F23 => F = F12 + F23 = 1,6 + 3,6 = 5,2 (N)
Trường hợp b2,b3 làm tương tự.

a) Lực tương tác giữa 2 điện tích là:
\(F=9.10^9.\frac{\left|4.10^{-7}.4.10^{-7}\right|}{0,05^2}=0,576\left(N\right)\)
b) 1) bạn tự vẽ hình
ta có: CA+CB=AB
=> C nằm trên đoạn AB
Lực điện do q1,q2 tác dụng lên q3
\(\overrightarrow{F_{13}}\) \(\left\{{}\begin{matrix}\text{phương chiều như hv}\\F_{13}=9.10^9.\frac{\left|4.10^{-7}.\left(-4.10^{-7}\right)\right|}{0,03^2}=1,6\left(N\right)\end{matrix}\right.\)
\(\overrightarrow{F_{23}}=9.10^9.\frac{\left|4.10^{-7}.\left(-4.10^{-7}\right)\right|}{0,02^2}=3,6\left(N\right)\)
Ta có : \(\overrightarrow{F}=\overrightarrow{F_{13}}+\overrightarrow{F_{23}}\)
Theo hv: \(\overrightarrow{F_{13}}\uparrow\downarrow\overrightarrow{F_{23}}\)
=> \(\left\{{}\begin{matrix}F=\left|F_{13}-F_{23}\right|=2\left(N\right)\\\overrightarrow{F}\uparrow\uparrow\overrightarrow{F_{23}}\end{matrix}\right.\)
Phần 2 và 3 lm tương tự nha bạn. Nếu k giải dc thì ib mik

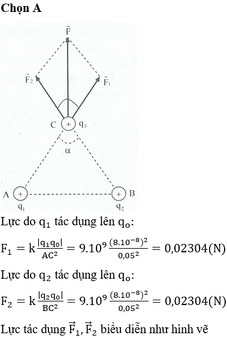
1/
CA=4cm; CB=10 cm
\(F_1=\dfrac{k\left|q_1q_3\right|}{AC^2}\left(N\right);F_2=\dfrac{k\left|q_2q_3\right|}{BC^2}\)
\(\Rightarrow\sum F=\left|F_1-F_2\right|=...\left(N\right)\)
AC=CB=5cm
\(AB^2=AC^2+BC^2-2.AC.BC.\cos\alpha\Rightarrow\alpha=....\)
\(F_1=\dfrac{k\left|q_1q_3\right|}{AC^2}\left(N\right);F_2=\dfrac{k\left|q_2q_3\right|}{BC^2}\left(N\right)\)
\(\sum F=\sqrt{F_1^2+F_2^2+2.F_1F_2.\cos\left(180^0-\alpha\right)}=...\left(N\right)\)

a/
+ + A B + C q1 q2 q3 F F F 23 13 hl → → →
Ta có: \(\vec{F_{hl}}=\vec{F_{13}}+\vec{F_{23}}\)
Do \(\vec{F_{13}}\uparrow\downarrow\vec{F_{23}}\) nên: \(F_{hl}=\left|F_{13}-F_{23}\right|\) (1)
\(F_{13}=9.10^9\frac{\left|q_1q_2\right|}{AC^2}=0,045N\)
\(F_{23}=9.10^9\frac{\left|q_1q_2\right|}{BC^2}=0,01N\)
Thay vào (1) ta được \(F_{hl}=0,035N\)
b/
+ + + A B D q1 q2 q3 F F F 23 13 hl → → →
Hợp lực: \(\vec{F_{hl}}=\vec{F_{13}}+\vec{F_{23}}\)
Do hai lực cùng phương cùng chiều nên độ lớn:
\(F_{hl}=F_{13}+F_{23}\)(2)
\(F_{13}=9.10^9.\frac{\left|q_1q_3\right|}{AD^2}=7,2.10^{-3}N\)
\(F_{23}=9.10^9.\frac{\left|q_2q_3\right|}{BD^2}=0,9.10^{-3}N\)
Thế vào (2) ta được \(F_{hl}=8,1.10^{-3}N\)