Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Có F = − k x = − k A cos ( ω t + φ ) = k A cos ( ω t + φ − π )
Từ đồ thị ta thấy:
+ t = 0 thì F = − F 0 2 và đang tăng ⇒ φ − π = − 2 π 3 ⇒ φ = π 3
+ T 2 = 13 6 − 7 6 = 1 ⇒ T = 2 ( s ) ⇒ ω = π ( r a d / s )
+ F m ax = 4.10 − 2 ( N ) ⇒ k A = 0 , 04 ( N ) ⇒ m ω 2 A = 0 , 04 ⇒ A = 4 ( c m )
Pt dao dộng: x = 4 cos π t + π 3 ( c m )

Đáp án A
Phương pháp: Áp dụng công thức tính lực kéo về vật dao động điều hoà: F = - kx = - m ω 2 x
Cách giải:
Khi t = 0,5s thì x = -10cm
Lực kéo về tác dụng lên vật: F = - kx = - m ω 2 x = 1N

\(k=\omega^2.m=\left(10\sqrt{10}\right)^2.0,2=200\)
Tại thời điểm t, vận tốc của vật có độ lớn: \(v=\dfrac{p}{m}=\dfrac{0,1\sqrt{10}}{0,2}=0,5\sqrt{10}\left(\dfrac{m}{s}\right)=50\sqrt{10}\left(\dfrac{cm}{s}\right)\)
Tại tời điểm t + T/2 vật có li độ: \(x=\dfrac{10\sqrt{3}}{200}.100=5\sqrt{3}\left(cm\right)\)
Ta có: \(\omega=\dfrac{v_t}{x_{t+\dfrac{T}{2}}}=\dfrac{50\sqrt{10}}{5\sqrt{3}}\ne10\sqrt{10}\)
Sai ở đâu không nhỉ ?

Giả sử: \(\pi^2\approx10\)
a) Khối lượng của vật: \(m=\dfrac{k}{\omega^2}=\dfrac{50}{\left(5\pi\right)^2}=0,2kg=200g\)
Chu kì của con lắc: \(T=\dfrac{2\pi}{\omega}=\dfrac{2}{5}\left(s\right)\)
b)Thế năng: \(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}\cdot50\cdot0,02^2=0,01J\)
Tại li độ \(x=2cm\) thì \(v=-\omega Asin\left(\pi t+\varphi\right)=-50\pi sin\left(5\pi t+\dfrac{\pi}{2}\right)\Rightarrow t\)
Động năng: \(W_đ=\dfrac{1}{2}mv^2\)
Cơ năng con lắc: \(W=W_đ+W_t=0,24J\)
a) \(k=m\omega^2=50\Rightarrow m=0,2\left(kg\right)\)
\(T=\dfrac{2\pi}{\omega}=0,4\left(s\right)\)
b) \(W_t=\dfrac{1}{2}kx^2=0,01\left(J\right)\)
\(W=\dfrac{1}{2}kA^2=0,25\left(J\right)\)
\(W_đ=W-W_t=0,24\left(J\right)\)
c) \(\Delta l=\dfrac{mg}{k}=0,04\left(m\right)\)
\(v=\dfrac{1}{2}v_{max}\Rightarrow x=\dfrac{A\sqrt{3}}{2}=5\sqrt{3}\left(cm\right)=0,05\sqrt{3}\left(m\right)\)
\(F_{đh}=k\left(\Delta l+x\right)\approx6,33\left(N\right)\)




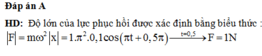
Lực kéo về: \(F=-k.x=-m.\omega^2.x=-1.\pi^2.0,1\cos(\pi.0,5-\pi/2)=-1(N)\)