Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có: ab=2; ac+ bd = 2
=> ab+cd=2=>2-ab=cd=1
vậy 1-cd=0 thì ko phải là số âm

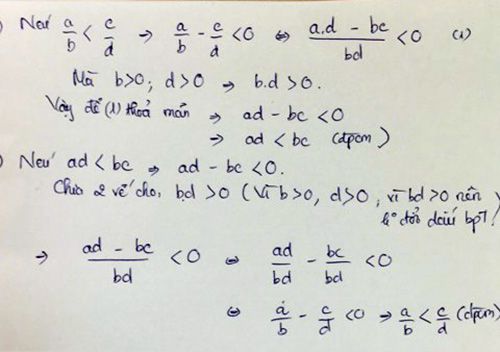
Làm nhắn gọn hơn thì
1
a/b < c/d
=> ad/bd < cb/db
=> ad < cb
2
ad < cb
=>ad /bd < cb/bd
Chúc pn hc tốt

Với a,b \(\in\)Z, b >0.
Ta có : a < b
\(\Rightarrow\)a + ab < b + ab
\(\Rightarrow\)a(b+1) < b(a+1)
\(\Rightarrow\)\(\frac{a}{b}< \frac{a+1}{b+1}\)
trả lời :
a/b < a+1/b+1
vì:
a cũ sẽ nhỏ hơn a mới 1 đơn vị
b cũ cũng sẽ nhỏ hơn b mới 1 đơn vị
mà a<b
nên có thể a + 1 sẽ = b cũ
ví dụ:
a=5
b=6
thì ta có:
5/6 và 5+1/6+1
=>5/6 và 6/7
nếu quy đồng 2 mẫu số thì ta có:
35/42 và 36/42
mà35/42 < 36/42
=> a/b < a+1/b+1

bạn viết lại đề bại giùm đc ko
\(0\le a\le b;1\le c...abc=1\)Số 2 là gì vậy

Ta có :
\(ab-c=ab-a+a-c=a\left(b-1\right)+\left(a-c\right)\)
\(\Rightarrow\left|ab-c\right|=\left|a\left(b-1\right)+\left(a-c\right)\right|\)
\(\Rightarrow\left|ab-c\right|\le\left|a\left(b-1\right)\right|+\left|a+c\right|\)
\(\Rightarrow\left|ab-c\right|\le\left|a\right|\left|b-1\right|+\left|a-c\right|\)
Mà \(\left|a\right|< 1;\left|b-1\right|< 10;\left|a-c\right|< 10\)
\(\Rightarrow\left|ab-c\right|< 1.10+10\)
\(\Rightarrow\left|ab-c\right|< 20\left(đpcm\right)\)

có \(\left|a\right|< 1\),\(\left|b-1\right|< 10\)suy ra \(\left|a\right|.\left|b-1\right|< 10\Rightarrow\left|a\left(b-1\right)\right|< 10\Leftrightarrow\left|ab-a\right|< 10\)
\(\Leftrightarrow-10< ab-a< 10\)(1)
có \(\left|a-c\right|< 10\Leftrightarrow-10< a-c< 10\)(2)
cộng lần lượt các vế của (1) và (2) ta có \(-10+\left(-10\right)< ab-a+a-c< 10+10\Leftrightarrow-20< ab-c< 20\)
suy ra \(\left|ab-c\right|< 20\)
co a<b+c<a+1 => a-c<b+c-c<a+1-c => a-c<b<a+1-c
ma a >1 b<c suy ra a phai lon hon c
ma c>b suy ra a>b