Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

85 km=8500000cm
Tỉ lệ trên bản đồ là:
17:8500000=2/1000000=1/500000
Khoảng cách thực tế giữa 2 điểm A và B là:
12:1/500000=6000000(cm)=60km
ĐS:60 km
Gọi x là khoảng cách giửa A và B trên thực tế
Với khoảng cách giữa hai thành phố = 85 ----------> khoảng cách trên bản đồ là 17
=>khoảng cách giữa A và B = x ----------> khoảng cách trên bản đồ là 12
Ta được tỷ số:
\(\frac{85}{x}=\frac{17}{12}\) => x = \(x=85.12:17=60\)
Vậy x = 60 => khoảng cách của A và B trên thực tế là 60km

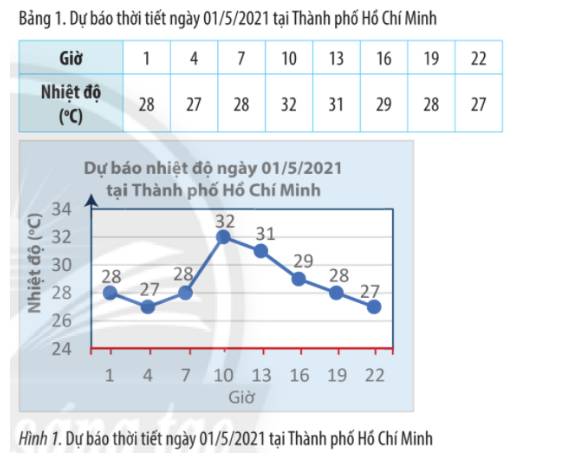
a) Tập hợp các mốc giờ đã có dự báo nhiệt độ là:
\(A = \{ 1;4;7;10;13;16;19;22\} \)
b) Tập hợp các số đo nhiệt độ đã dự báo là:
\(B = \{ 28;27;32;31;29\} \)
c) Dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021 nhiệt độ là \({28^o}C.\)

không hiểu nổi tại sao lại là 2 lần đường.
XA XB A B C : Lần gặp 1 c: lần gặp 2 xe XA còn qua đoạn CA nữa mới đủ 2 lần xe XB còn qua đoạn CB nữa mới đủ 2 lần tính đến lúc gặp nhau lần 2
Xin lỗi, vì khi cái này đăng lên, câu hỏi trên sẽ bị loại khỏi danh sách "chưa trả lời"

Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
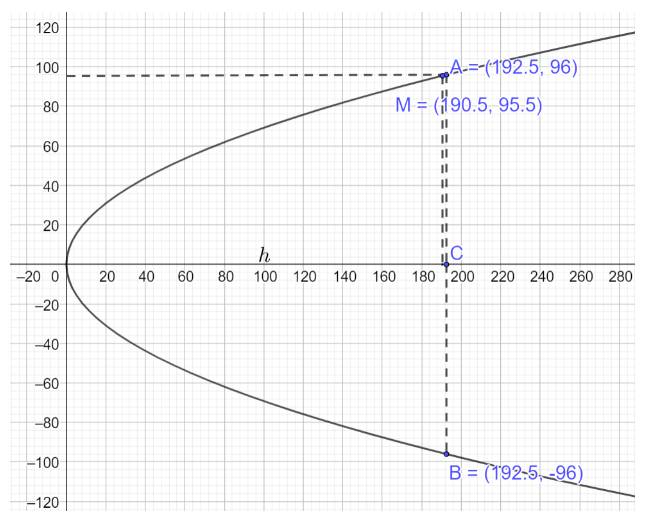
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h - 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h - 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m

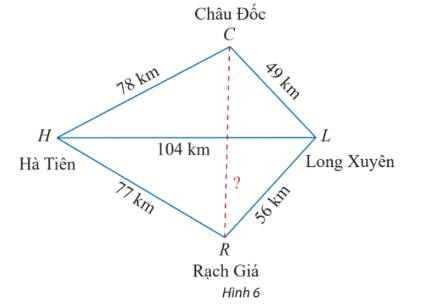
Bước 1: Áp dụng hệ quả của định lí cosin trong tam giác HCL, ta có:
\(\begin{array}{l}\cos \;\widehat {CHL} = \frac{{C{H^2} + H{L^2} - C{L^2}}}{{2.CH.HL}} = \frac{{{{78}^2} + {{104}^2} - {{49}^2}}}{{2.78.104}} = \frac{{4833}}{{5408}}\\ \Rightarrow \;\widehat {CHL} \approx {26^o}39'40,05''\end{array}\)
Áp dụng hệ quả của định lí cosin trong tam giác HLR, ta có:
\(\begin{array}{l}\cos \;\widehat {LHR} = \frac{{H{L^2} + H{R^2} - L{R^2}}}{{2.HL.HR}} = \frac{{{{104}^2} + {{77}^2} - {{56}^2}}}{{2.104.77}} = \frac{{13609}}{{16016}}\\ \Rightarrow \;\widehat {LHR} \approx {31^o}49'10,4''\\ \Rightarrow \;\widehat {CHR} \approx {58^o}28'50,45''\end{array}\)
Bước 2: Áp dụng định lí cosin \(C{R^2} = H{C^2} + H{R^2} - 2.HC.HR\cos \widehat {CHR}\)
\(\begin{array}{l} \Leftrightarrow C{R^2} = {78^2} + {77^2} - 2.78.77\cos {58^o}28'50,45''\\ \Rightarrow CR \approx 75,72\end{array}\)
Vậy khoảng cách giữa Châu Đốc và Rạch Giá là 75, 72 km.


Chọn B
Nguyễn Lê Phước Thịnh , làm thế nào vậy bro??