Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

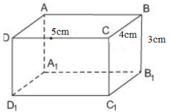
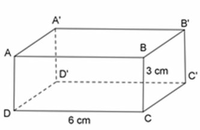
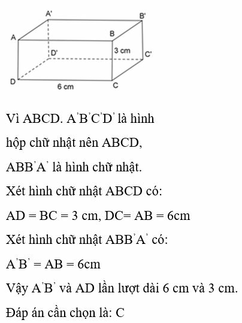
Vì ABCD.A1B1C1D1 là hình hộp chữ nhật
⇒ DCC1D1 và CBB1C1 là hình chữ nhật.
⇒ CC1 = BB1 = 3cm
ΔDCC1 vuông tại C, áp dụng định lí Py-ta–go ta có:
DC12 = DC2 + CC12
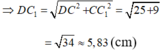
ΔCBB1 vuông tại B, áp dụng định lí Py–ta-go ta có:
CB12= CB2 + BB12
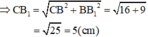

thể tích hình hộp chữ nhật là : V=\(3\sqrt{2}.4\sqrt{2}.5=120\) cm3

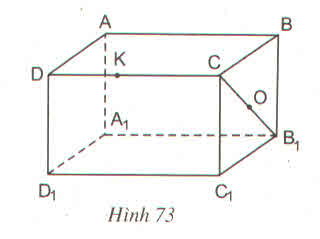
Với hình hộp chữ nhật ABCD. A 1B1C1D1
a) Nếu O là trung điểm của đoạn CB1 thì O cũng là trung điểm của đoạn C1B vì CBB1C1 là hình chữ nhật nên hai đường chéo có chung một trung điểm.
b) K là điểm thuộc cạnh CD thì K không thuộc cạnh BB1 vì bốn điểm C, D, B, B1 không thuộc một mặt phẳng

Thể tính hình hộp chữ nhật là:
\(V=3\sqrt{2}.4\sqrt{2}.5=120\left(cm^3\right)\)


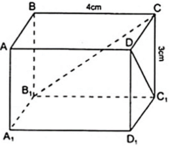
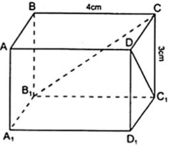
DC1 ∈ mp( DCC1D1 ) với D C C 1 D 1 là hình chữ nhật nên Δ DCC1 vuông tại C.
Áp dụng định lý Py – ta – go vào Δ DCC1 vuông tại C ta được: DC12 = CC12 + CD2
Hay DC12 = 32 + 52 ⇔ DC12 = ( √ (34) )2 ⇔ DC1 = √ (34) ( cm )
CB1 ∈ ( BCC1B1 ) là hình chữ nhật nên Δ BCB1 vuông tại B.
Áp dụng định lí Py – ta – go vào Δ BCB1 vuông tại B ta được: CB12 = CB2 + BB12
Hay CB12 = 32 + 42 = 52 ⇔ CB1 = 5( cm )
Vậy DC1 = √ (34) ( cm ); CB1 = 5( cm )

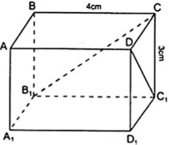

Vì ABCD.A1B1C1D1 là hình hộp chữ nhật nên DCC1D1 và CBB1C1 là hình chữ nhật.
=> CC1 = BB1 = 3cm