Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách giải:
Giải: Trong không khí vị trí vân sáng bậc 2 là: b 1 = 2 λ D a ; khoảng vân c 1 = λ D a
số vân sáng quan sát được trên màn là:
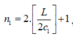
trong đó L là bề rộng trường giao thoa.
Làm thí nghiệm trên trong nước có chiết suất n > 1, với D,a và vị trí của S không đổi thì vị trí vân sáng bậc 2 là:
b
2
=
2
λ
D
n
a
; khoảng vân
c
1
=
λ
D
n
a
; số vân sáng quan sát được trên màn là:
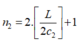
So sánh ta thấy: b1 > b2; c1 >c2; n1 < n2 => chọn B

Đáp án A
+ Khi tiến hành thí nghiệm trong nước có chiết suất n thì bước sóng xác định bởi:

+ Như vậy phải thay đổi khoảng cách từ mặt phẳng
chứa hai khe đến màn quan sát một lượng
![]()

Bạn click vào đây nhé: Câu hỏi của Hiếu - Học và thi online với HOC24

Tại vân tối thứ k của 1 bức xạ nào đó có N vân sáng, ta có: \(x=(k+0,5)i=k'.i'\)(*)
Trong môi trường chiết suất n thì bước sóng, khoảng vân giảm đi n lần.
Khi đó, \(i=2i_1;i'=2i_1'\)
Thay vào (*) ta được: \(x=(2k+1)i_1=2k'i_1'\)(**)
Biểu thức (**) đều là điều kiện cho vân sáng.
Như vậy, ta sẽ có (N+1) vân sáng.

Chọn A
Tại vị trí M trên màn, cách vân sáng trung tâm một đoạn 4,4 mm là vân tối thứ 6 tức là: x = 5,5i = 4,4mm => i = 0,8mm.
bước sóng λ của ánh sáng đơn sắc trong thí nghiệm là:
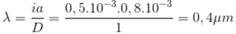

Đáp án C
+ Khoảng vân giao thoa của hai bức xạ i 1 = D λ 1 a = 2.0 , 5.10 − 6 1.10 − 3 = 1 mm, i 2 = D λ 2 a = 2.0 , 3.10 − 6 1.10 − 3 = 0 , 6 mm
→ Số vị trí cho vân sáng ứng với các bức xạ lần lượt là
N s 1 = 2 L 2 i 1 + 1 = 2 14 , 2 2.1 + 1 = 15 ; N s 2 = 2 L 2 i 2 + 1 = 2 14 , 2 2.0 , 6 + 1 = 23
Vị trí trùng nhau của các vân sáng của hai hệ vân k 1 k 2 = λ 2 λ 1 = 3 5 → trên đoạn A B có các vị trí trùng nhau tương ứng
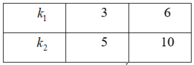
Mỗi vị trí trùng ta tính là một vân sáng, có tất cả 5 vị trí trùng – tính cả vân trung tâm → số vạch sáng quan sát được là N = 15 + 23 − 5 = 33
