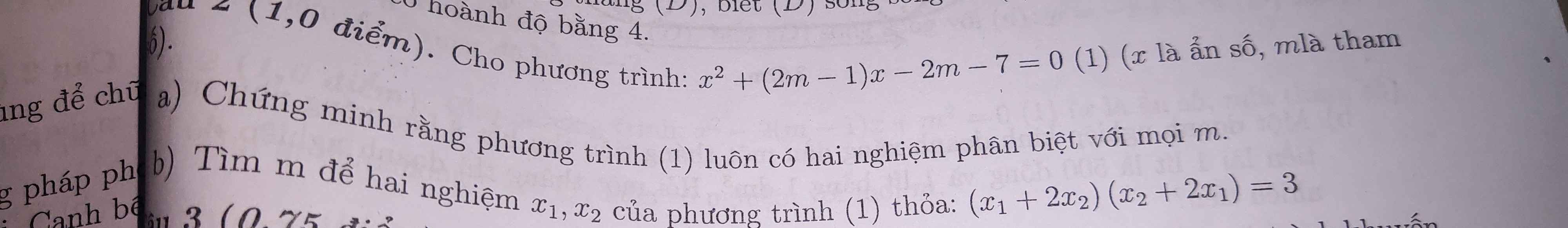Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m+1\\x_1x_2=-2m-7\end{matrix}\right.\)
\(\left(x_1+2x_2\right)\left(x_2+2x_1\right)=3\)
\(\Leftrightarrow2x_1^2+2x_2^2+5x_1x_2=3\)
\(\Leftrightarrow2\left(x_1+x_2\right)^2+x_1x_2=3\)
\(\Leftrightarrow2\left(-2m+1\right)^2+\left(-2m-7\right)=3\)
\(\Leftrightarrow4m^2-5m-4=0\) \(\Rightarrow m=\dfrac{5\pm\sqrt{89}}{8}\)

Ủa , 0 + 0 = 0 mà !
Đến cả đứa 5 tuổi cũng biết mà sao cậu không giải được ?

<=>\(\left(\sqrt{\sqrt{2}+1}-\sqrt{\sqrt{2}-1}\right)^2=\left(\sqrt{2\left(\sqrt{2}-1\right)}\right)^2\)
<=>\(\sqrt{2}+1+\sqrt{2}-1-2\left(\sqrt{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}\right)=2\left(\sqrt{2}-1\right)\)
<=>\(2\sqrt{2}-2=2\sqrt{2}-2\left(dpcm\right)\)
¬¬¬¬¬¬hoc tot ¬¬¬¬¬¬¬

\(P=\left(\dfrac{x-1}{\sqrt{x}+1}-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}}+1\right).\dfrac{1}{x\sqrt{x}+1}\)
\(=\left(\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}+1}-\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)}+1\right).\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\left(\sqrt{x}-1-\dfrac{\sqrt{x}-1}{\sqrt{x}}+1\right).\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)+\sqrt{x}}{\sqrt{x}}.\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}.\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}=\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
Bài 2:
Ta có: \(P=\left(\dfrac{x-1}{\sqrt{x}+1}-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}}+1\right)\cdot\dfrac{1}{x\sqrt{x}+1}\)
\(=\left(\sqrt{x}-1-\dfrac{\sqrt{x}-1}{\sqrt{x}}+1\right)\cdot\dfrac{1}{x\sqrt{x}+1}\)
\(=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{1}{x+\sqrt{x}}\)