Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

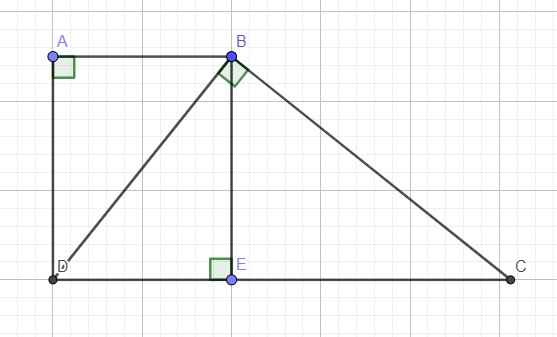
Kẻ BE vuông góc CD \(\Rightarrow ABED\) là hcn (tứ giác 4 góc vuông) \(\Rightarrow AB=DE\)
Đặt \(AB=x>0\)
Áp dụng định lý Pitago cho tam giác vuông ABD:
\(AB^2+AD^2=BD^2\Leftrightarrow BD^2=x^2+144\) (1)
Áp dụng hệ thức lượng cho tam giác vuông BDC:
\(BD^2=DE.DC\Leftrightarrow BD^2=25x\) (2)
(1);(2) \(\Rightarrow x^2+144=25x\Rightarrow x^2-25x+144=0\Rightarrow\left[{}\begin{matrix}x=16\\x=9\end{matrix}\right.\)
- Với \(AB=16\left(cm\right)\Rightarrow BD=\sqrt{AD^2+AB^2}=20\left(cm\right)\)
\(BC=\sqrt{DC^2-BD^2}=15\left(cm\right)\)
- Với \(AB=9\left(cm\right)\Rightarrow BD=\sqrt{AD^2+AB^2}=15\left(cm\right)\)
\(BC=\sqrt{DC^2-BD^2}=20\left(cm\right)\)

Áp dụng các hệ thức lượng trong tam giác vuông BDC cùng chú ý độ dài đường cao hạ từ B xuống CD bằng AD, ta tính được : AB = 9cm, BD =15cm, hoặc AB = 16cm, BC = 15cm, BD = 20cm

Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
Do góc <DAB = <CBD =90 độ và <ABD = < BDC (do AB//CD)
-> Tam giác ADB và BCD đồng dạng
=> AD/BC = DB/CD <-> AD.CD=BC.DB <-> BC.DB = 12.25 =300 (1)
Mặt khác do tam giác DBC vuông tại B nên theo định lý Pitago :
BD^2+BC^2=CD^2
hay BC^2+BD^2 =625 (2)
Từ (1) và (2) ta giải hệ thì có BC, BD:
BD^2+ (300/BD)^2=625 -> BD^4 - 625 BD^2 +900 = 0 -> BD^2 = (625+can( 387025))/2 ( loại nghiệm còn lại do BD là cạnh huyền của tam giác vuông ABD nên BD^2 > AD^2 =144)
-> BD = can( (625+can( 387025))/2 )
-> BC = 3000/BD
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~ Và chúc các bạn trả lời câu hỏi này kiếm được nhiều k hơn ~~~~~~~~~~~~

Tham Khảo tại link
https://hoc24.vn/cau-hoi/cho-abcd-la-hinh-thang-vuong-tai-a-va-d-duong-cheo-bd-vuong-goc-voi-bc-biet-ad-12-cm-dc-25-cm-tinh-do-dai-ab-bc-bd.189488030358
Hạ BE ⊥ CD ( E ∈ CD )
Xét △BCD vuông tại B có BE ⊥ CD. Áp dụng hệ thức lượng trong tam giác vuông, ta có:
BE\(^2\) = DE . EC hay DE . ED = 12\(^2\) =144 cm (*)
Ta có:
DE + EC = CD = 25 cm ⇒ DE = 25 − EC
Thay vào (*) ta có: ( 25 − EC ) . EC = 144
⇒ 25 EC − EC\(^2\) = 144
⇒ EC\(^2\) − 25 EC + 144 = 0
⇒ ( EC − 9 )( EC − 16 ) = 0
\(\Rightarrow\left[{}\begin{matrix}EC=9\\EC=16\end{matrix}\right.\)
Nếu EC = 9 cm ⇒ DE = 16 cm
Xét tứ giác ABED có ˆ\(\widehat{A}=\widehat{D}=\widehat{E}=90^0\) nên là hình chữ nhật
⇒ AB = DE ; AD = BE
Hay AB = 16 cm và BE = 12cm
Áp dụng định lý Pytago trong tam giác vuông BED ta có: \(BD^2=BE^2+DE^2=12^2+16^2=400\) ⇒ BD = 20 cm
Áp dụng định lý Pytago trong tam giác vuông BEC, ta có: \(BC^2=BE^2+CE^2=12^2=92=225\)
⇒ BC = 15 cm
Tương tự với trường hợp EC = 16cm ⇒ DE = 9 cm
Ta suy ra: AB = 9 cm ; BD = 15 cm và BC = 20 cm