Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5

A = 2 + 22 + 23 + 24 + ... + 219 + 220
A = (2 + 22) + (23 + 24) +... + (219 + 220)
A = 2.(1+2) + 23.(1 + 2) +... + 219.(l + 2)
A = 2.3 + 23.3 +...+ 219.3 Do đó A chia hết cho 3

A=\((1+2)+\left(2^2+2^3\right)+...+\left(2^{19}+2^{20}\right)\)
A=\(3.1+2^2\left(1+2\right)+...+2^{19}\left(1+2\right)\)
A=\(3.1+3.2^2+...+3.2^{19}\)
A=\(3\left(1+2^2+...+2^{19}\right)\)\(⋮3\)
Vậy A\(⋮3\)
A=(1+2)+(22+23)+...+(219+220)(1+2)+(22+23)+...+(219+220)
A=3.1+22(1+2)+...+219(1+2)3.1+22(1+2)+...+219(1+2)
A=3.1+3.22+...+3.2193.1+3.22+...+3.219
A=3(1+22+...+219)3(1+22+...+219)⋮3⋮3
NÊN A⋮3

a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:

![]()
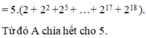

\(A=\left(3+3^2+3^3\right)+...+\left(3^{58}+3^{59}+3^{60}\right)\\ A=3\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\\ A=\left(1+3+3^2\right)\left(3+...+3^{58}\right)\\ A=13\left(3+...+3^{58}\right)⋮13\)
\(M=\left(2+2^2+2^3+2^4\right)+...+\left(2^{17}+2^{18}+2^{19}+2^{20}\right)\\ M=\left(2+2^2+2^3+2^4\right)+...+2^{16}\left(2+2^2+2^3+2^4\right)\\ M=\left(2+2^2+2^3+2^4\right)\left(1+...+2^{16}\right)\\ M=30\left(1+...+2^{16}\right)⋮5\)

Bài 1
a, cm : A = 165 + 215 ⋮ 3
A = 165 + 215
A = (24)5 + 215
A = 220 + 215
A = 215.(25 + 1)
A = 215. 33 ⋮ 3 (đpcm)
b,cm : B = 88 + 220 ⋮ 17
B = (23)8 + 220
B = 216 + 220
B = 216.(1 + 24)
B = 216. 17 ⋮ 17 (đpcm)
c, cm: C = 1 - 2 + 22 - 23 + 24 - 25 + 26 -...-22021 + 22022 : 6 dư 1
C=1+(-2+22-23+24- 25+26)+...+(-22017+22018-22019+22020-22021+22022)
C = 1 + 42 +...+ 22016.(-2 + 22 - 23 + 24 - 25 + 26)
C = 1 + 42+...+ 22016.42
C = 1 + 42.(20+...+22016)
42 ⋮ 6 ⇒ C = 1 + 42.(20+...+22016) : 6 dư 1 đpcm
A=2+22+23+...+220
a) Vì cơ số của mỗi lũy thừa là 2 => A chia hết cho 2
b)A=2+22+23+...+220
A=(2+22)+(23+24)+...+(219+220 )
A=(2+22)+23(2+22)+...+219(2+22 )
A=6+23x6+...+219x6
A=6x(1+23+...+219)
Vì 6 chia hết cho 3=> A chia hết cho 3
HT