Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A C D B
Ta có:
Vì AB // CD
=> ^A,^D ; ^B,^C là 2 cặp góc trong cùng phía với nhau
=> \(\hept{\begin{cases}\widehat{A}+\widehat{D}=180^0\\\widehat{B}+\widehat{C}=180^0\end{cases}}\Leftrightarrow\hept{\begin{cases}\widehat{D}+20^0+\widehat{D}=180^0\\2\cdot\widehat{C}+\widehat{C}=180^0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2\cdot\widehat{D}=160^0\\3\cdot\widehat{C}=180^0\end{cases}\Leftrightarrow}\hept{\begin{cases}\widehat{D}=80^0\\\widehat{C}=60^0\end{cases}\Rightarrow}\hept{\begin{cases}\widehat{A}=100^0\\\widehat{B}=120^0\end{cases}}\)
Vậy \(\widehat{A}=100^0\) ; \(\widehat{B}=120^0\) ; \(\widehat{C}=60^0\) ; \(\widehat{D}=80^0\)
Ta có:\(\widehat{A}+\widehat{D}=180^o\left(TCP\right)\left(1\right)\)
\(\widehat{A}-\widehat{D}=20^o\left(2\right)\)\(\Rightarrow\widehat{A}=20^o+\widehat{D}\)thế vào \(\left(1\right)\),Ta đc:
\(20^o+\widehat{D}+\widehat{D}=180^o\)
\(2\widehat{D}=160^o\)
\(\widehat{D}=160^o\div2=80^o\)
\(\widehat{A}=20^o+\widehat{D}=20^o+80^o=100^o\)
\(\widehat{B}+\widehat{C}=180^o\left(3\right)\)
\(\widehat{B}=2\widehat{C}\left(4\right)\)
Thế (4) vào (3) ta được:
\(2\widehat{C}+\widehat{C}=180^o\)
\(3\widehat{C}=180^o\)
\(\widehat{C}=60^o\)
\(\widehat{B}=2\widehat{C}=2.60^o=180^o\)
Vậy...

a) Vì AB//CD, ta có góc ACD = góc BCD = 180 - góc D = 180 - 60 = 120 độ.
Vì AB//CD, ta có góc ACD = góc BAD.
Vậy số đo góc A là 120 độ.
b) Gọi góc BCD là x độ.
Theo giả thiết, góc B phần góc D = 4/5, ta có:
góc B = (4/5) * góc D
= (4/5) * 60
= 48 độ.
Vì AB//CD, ta có góc BCD = góc BAD.
Vậy góc BAD = góc BCD = x độ.
Vì tứ giác ABCD là tứ giác lồi, tổng các góc trong tứ giác ABCD là 360 độ.
Ta có: góc A + góc B + góc C + góc D = 360 độ.
Vì góc D = 60 độ, góc A = 120 độ và góc B = 48 độ, ta có:
120 + 48 + góc C + 60 = 360
góc C = 360 - 120 - 48 - 60 = 132 độ.
Vậy số đo góc B là 48 độ và số đo góc C là 132 độ.
* Ib = bài 4

a) Sử dụng tính chất dãy tỉ số bằng nhau. A ^ = 144 0 , B ^ = 108 0 , C ^ = 72 0 , D ^ = 36 0
b) Sử dụng tổng ba góc trong tam giác tính được C E D ^ = 126 0 .
Chú ý hai phân giác trong và ngoài tại mỗi góc của một tam giác thì vuông góc nhau, cùng với tổng bốn góc trong tứ giác, ta tính được C F D ^ = 54 0
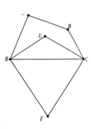

A B C D E F 1 1 2 2
Xét Tứ giác ABCD có: góc A + B + C + D = 360o => 100o + 120o + (C + D) = 360o => góc C + D = 140o
DE; CE lần lượt là p/g của góc D; C => góc D1 = D/ 2 ; C1 = C/ 2 => góc (D1 + C1) = (D + C) /2 = 700
Xét tam giác DEC có: góc D1 + góc E + góc C1 = 180o => góc DEC = 180o - (D1 + C1) = 180o - 70o = 110o
Vì tia Dx là p/g ngoài của góc D; DE là p/g trong của góc D => Dx vuông góc với DE => DF vuông góc với DE => góc EDF = 900
=> góc D2 = 90o - D1
Vì tia Cy là p/g ngoài của góc ACD ; CE là p/g trong của góc ACD => Cy vuông góc với CE => CF vuông góc với CE => góc ECF = 90o
=> góc C2 = 90o - C1
Xét tam giác CDF có: góc C2 + góc CFD + góc D2 = 180o
=> góc CFD + (90o - D1 + 90o - C1) = 180o => góc CFD + 180o - (D1 + C1) = 180o => góc CFD = D1 + C1 = 90o