Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

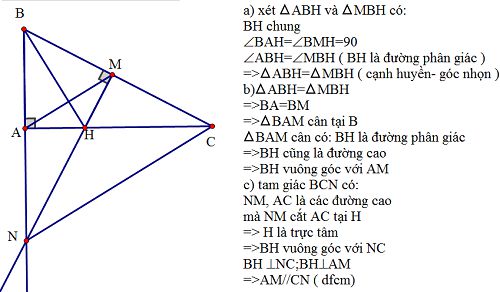
a) xét tam giác ABH và taam giác MBH có :
AB=BH(BE là tia phân giác)
ABH=HBM(BE là tia phân giác)
BH cạnh chung
=>tam giác ABH =tam giácHBE (c.g c)
b)=>tam giác ABM cân tại B mà BH là phân giác
=>BE là trung trực
=>AHB=MHB=90 độ
c)vì AMC và góc MNC là cặp góc so le trong
=>AM//NC
d)Vì AM//NC(theo c)
mà BH vuông góc với AM
=>BH vông góc với NC (T/C từ vuông góc đến song song)
a) xét tam giác ABH và taam giác MBH có :
AB=BH(BE là tia phân giác)
ABH=HBM(BE là tia phân giác)
BH cạnh chung
=>tam giác ABH =tam giácHBE (c.g c)
b)=>tam giác ABM cân tại B mà BH là phân giác
=>BE là trung trực
=>AHB=MHB=90 độ
c)vì AMC và góc MNC là cặp góc so le trong
=>AM//NC
d)Vì AM//NC(theo c)
mà BH vuông góc với AM
=>BH vông góc với NC (T/C từ vuông góc đến song song)

3/ (Bạn tự vẽ hình giùm. Vẽ hình dễ)
a/ \(\Delta ACE\)vuông và \(\Delta AKE\)vuông có: \(\widehat{CAE}=\widehat{EAK}\)(AE là đường phân giác của \(\Delta ABC\))
Cạnh huyền AE chung
=> \(\Delta ACE\)vuông = \(\Delta AKE\)vuông (cạnh huyền - góc nhọn) (đpcm)
b/ Ta có \(\Delta ACE\)= \(\Delta AKE\)(cm câu a) => AC = AK (hai cạnh tương ứng)
Gọi M là giao điểm của AE và CK.
\(\Delta ACM\)và \(\Delta AKM\)có: AC = AK (cmt)
\(\widehat{CAM}=\widehat{MAK}\)(AM là đường phân giác của \(\Delta ABC\))
Cạnh AM chung
=> \(\Delta ACM\)= \(\Delta AKM\)(c - g - c) => CM = KM (hai cạnh tương ứng) (1)
và\(\widehat{AMC}=\widehat{AMK}\)(hai góc tương ứng)
Mà \(\widehat{AMC}+\widehat{AMK}\)= 180o (kề bù)
=> 2\(\widehat{AMC}\)= 180o
=> \(\widehat{AMC}\)= 90o
=> AM \(\perp\)CK (2)
Từ (1) và (2) => AE là đường trung trực của CK (đpcm)