Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
\(2n+1⋮n-3\)
\(\Rightarrow\left(2n-6\right)+7⋮n-3\)
\(\Rightarrow2\left(n-3\right)+7⋮n-3\)
\(\Rightarrow7⋮n-3\)
\(\Rightarrow n-3\in\left\{1;7\right\}\) ( Vì \(n\in N\) )
\(\Rightarrow\left\{{}\begin{matrix}n-3=1\Rightarrow n=4\\n-3=7\Rightarrow n=10\end{matrix}\right.\)
Vậy n=4 hoặc n=10
b) Ta có:
\(n^2+3n-13⋮n+3\)
\(\Rightarrow n\left(n+3\right)-13⋮n+3\)
\(\Rightarrow-13⋮n+3\)
\(\Rightarrow n+3\in\left\{1;13\right\}\) ( Vì \(n\in N\) )
\(\Rightarrow\left\{{}\begin{matrix}n+3=1\Rightarrow n=-2\left(loai\right)\\n+3=13\Rightarrow n=10\end{matrix}\right.\)
Vậy n=10
c) Ta có:
\(n^2+3⋮n-1\)
\(\Rightarrow n^2-1+4⋮n-1\)
\(\Rightarrow\left(n-1\right)\left(n+1\right)+4⋮n-1\)
\(\Rightarrow n+1+4⋮n-1\)
\(\Rightarrow n+5⋮n-1\)
\(\Rightarrow\left(n-1\right)+6⋮n-1\)
\(\Rightarrow6⋮n-1\)
\(\Rightarrow n-1\in\left\{1;2;3;6\right\}\) ( Vì \(n\in N\) )
\(\Rightarrow\left\{{}\begin{matrix}n-1=1\Rightarrow n=2\\n-1=2\Rightarrow n=3\\n-1=3\Rightarrow n=4\\n-1=6\Rightarrow n=7\end{matrix}\right.\)
Vậy n=2 hoặc n=3 hoặc n=4 hoặc n=7
a,\(2n+1=2n-6+7=2\left(n-3\right)+7\)
Do \(2\left(n-3\right)⋮n-3\)
\(\Rightarrow n-3\in\left\{\pm1;\pm7\right\}\)
\(\Leftrightarrow\left[{}\begin{matrix}n-3=1\\n-3=-1\\n-3=7\\n-3=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}n=4\\n=2\\n=10\\n=-4\end{matrix}\right.\)

a) 172123=(1724)30.1723
Ta thấy 1724 có tận cùng bằng 6 => (1724)30 có tận cùng bằng 6
1723 có tận cùng bằng 8
=> 172123 có tận cùng bằng 8
Mình giải một dạng thôi ;
2) \(3^x+3^{x+1}=36\\ \Rightarrow3^x\left(1+3\right)=36\\ \Rightarrow3^x=9\\ \Rightarrow x=2\)
b) \(2^x\left(1+2+2^2+2^3\right)=120\\ \Rightarrow2^x=8\\ \Rightarrow x=3\)
c) Khó

b) Ta có:
\(2^{3n}=\left(2^3\right)^n=8^n\)
\(3^{2n}=\left(3^2\right)^n=9^n\)
Vì \(8^n< 9^n\Rightarrow2^{3n}< 3^{2n}\)
Vậy \(2^{3n}< 3^{2n}\)


\(3n+2=3n-12+14=\left(-3\right)\left(4-n\right)+14\\ \left(-3\right)\left(4-n\right)⋮4-n\\ \text{Để }3n+2⋮4-n\Rightarrow14⋮4-n\Rightarrow4-n\inƯ\left(14\right)=\left\{-14;-7;-2;-1;1;2;7;14\right\}\)
| $ 4 - n $ | $ n $ |
| $ - 14 $ | $ 18 $ |
| $ - 7 $ | $ 11 $ |
| $ - 2 $ | $ 6 $ |
| $ - 1 $ | $ 5 $ |
| $ 1 $ | $ 3 $ |
| $ 2 $ | $ 2 $ |
| $ 7 $ | $ - 3 $ |
| $ 14 $ | $ - 10 $ |
Vậy \(n\in\left\{-10;-3;2;3;5;6;11;18\right\}\)
\(n^2+n+2=n^2-1+n-1+4=\left(n+1\right)\left(n-1\right)+\left(n-1\right)+4=\left(n-1\right)\left(n+2\right)+4\\ \left(n-1\right)\left(n+2\right)⋮n-1\\ \text{Để }n^2+n+2⋮n-1\Rightarrow4⋮n-1\Rightarrow n-1\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
| $ n - 1 $ | $ n $ |
| $ - 4 $ | $ - 3 $ |
| $ - 2 $ | $ - 1 $ |
| $ - 1 $ | $ 0 $ |
| $ 1 $ | $ 2 $ |
| $ 2 $ | $ 3 $ |
| $ 4 $ | $ 5 $ |
Vậy \(n\in\left\{-3;-1;0;2;3;5\right\}\)

(n^2 -9)(2n+6) =0
2(n-3)(n+3)^2=0
tương đương n-3= 0 và (n+3)^2=0
suy ra n=3 và n=-3
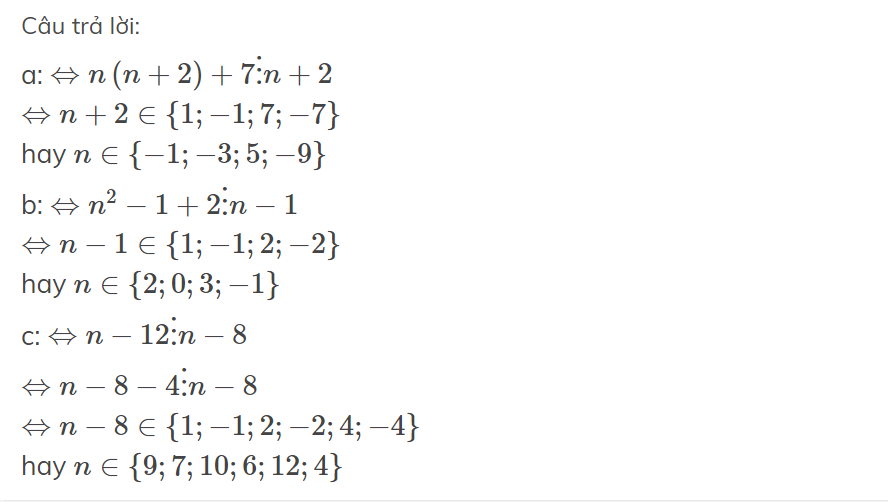

a) \(n+1\inƯ\left(n^2+2n-3\right)\)
\(\Leftrightarrow n^2+2n-3⋮n+1\)
\(\Leftrightarrow n\left(n+1\right)+n-3⋮n+1\)
Vì \(n\left(n+1\right)⋮n+1\Rightarrow n-3⋮n+1\)
\(\Leftrightarrow n+1-4⋮n+1\)
Vì \(n+1⋮n+1\Rightarrow-4⋮n+1\Rightarrow n+1\inƯ\left(-4\right)=\left\{-1;1;-2;2;-4;4\right\}\)
Ta có bảng sau:
Vậy...
b) \(n^2+2\in B\left(n^2+1\right)\)
\(\Leftrightarrow n^2+2⋮n^2+1\)
\(\Leftrightarrow n^2+1+1⋮n^2+1\)
Vì \(n^2+1⋮n^2+1\) nên \(1⋮n^2+1\Rightarrow n^2+1\inƯ\left(1\right)=\left\{-1;1\right\}\)
Ta có bảng sau:
\(0\) (tm)
Vậy \(n=0\)
c) \(2n+3\in B\left(n+1\right)\)
\(\Leftrightarrow2n+3⋮n+1\)
\(\Leftrightarrow2n+2+1⋮n+1\)
\(\Leftrightarrow2\left(n+1\right)+1⋮n+1\)
Vì \(2\left(n+1\right)⋮n+1\) nên \(1⋮n+1\Rightarrow n+1\inƯ\left(1\right)=\left\{-1;1\right\}\)
Ta có bảng sau:
Vậy...
a) n+1∈Ư(n2+2n−3)n+1∈Ư(n2+2n−3)
⇔n2+2n−3⋮n+1⇔n2+2n−3⋮n+1
⇔n(n+1)+n−3⋮n+1⇔n(n+1)+n−3⋮n+1
Vì n(n+1)⋮n+1⇒n−3⋮n+1n(n+1)⋮n+1⇒n−3⋮n+1
⇔n+1−4⋮n+1⇔n+1−4⋮n+1
Vì n+1⋮n+1⇒−4⋮n+1⇒n+1∈Ư(−4)={−1;1;−2;2;−4;4}n+1⋮n+1⇒−4⋮n+1⇒n+1∈Ư(−4)={−1;1;−2;2;−4;4}
Ta có bảng sau:
Vậy...
b) n2+2∈B(n2+1)n2+2∈B(n2+1)
⇔n2+2⋮n2+1⇔n2+2⋮n2+1
⇔n2+1+1⋮n2+1⇔n2+1+1⋮n2+1
Vì n2+1⋮n2+1n2+1⋮n2+1 nên 1⋮n2+1⇒n2+1∈Ư(1)={−1;1}1⋮n2+1⇒n2+1∈Ư(1)={−1;1}
Ta có bảng sau:
00 (tm)
Vậy n=0n=0
c) 2n+3∈B(n+1)2n+3∈B(n+1)
⇔2n+3⋮n+1⇔2n+3⋮n+1
⇔2n+2+1⋮n+1⇔2n+2+1⋮n+1
⇔2(n+1)+1⋮n+1⇔2(n+1)+1⋮n+1
Vì 2(n+1)⋮n+12(n+1)⋮n+1 nên 1⋮n+1⇒n+1∈Ư(1)={−1;1}1⋮n+1⇒n+1∈Ư(1)={−1;1}
Ta có bảng sau: