Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do đó, mỗi đường thẳng là đường phân giác của một góc bẹt.
a. Đúng
b. Đúng
c. Đúng

a) Hai đường thẳng xx' và yy' cắt nhau tại O : Đúng
b) Hai đường thẳng xx' và yy' tạo thành 4 góc vuông : Sai
c) Mỗi đường thẳng là đường phân giác của một góc bẹt : Đúng

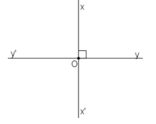
Ta có : – Góc x’Oy’ và góc xOy là hai góc đối đỉnh ⇒ góc xOy = góc x’Oy’ = 90o
– ∠(xOy) và ∠(xOy’) là hai góc kề bù ⇒ ∠(xOy) + ∠(xOy’) = 180o
⇒ (xOy’) = 180o – (xOy) = 180o– 90o = 90o
– ∠(xOy’) và ∠(x’Oy) là hai góc đối đỉnh ⇒ ∠(xOy’) = ∠(x’Oy) = 90o
Khi đó các góc ∠yOx’ ; ∠x’Oy’ ; ∠y’Ox cũng đều là những góc vuông
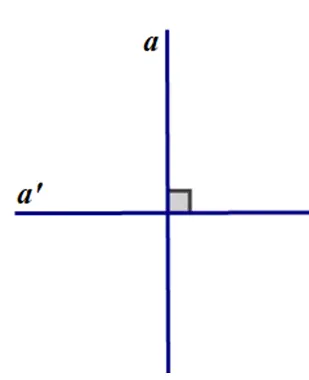
Trả lời câu hỏi Toán 7 Tập 1 Bài 2 trang 84: Vẽ phác hai đường thẳng a và a’ vuông góc với nhau và viết kí hiệu.
Lời giải

Chưa có ai trả lời câu hỏi này, hãy gửi một câu trả lời để giúp HitRuu Zero giải bài toán này.
Gửi câu trả lời của bạn
Bài 1: Điền vào chỗ trống trong các phát biểu sau
a) Hai đường thẳng vuông góc với nhau là hai đường thẳng ..................................
b) Có ........................ đường thẳng a' đi qua điểm O và vuông góc với đường a cho trước
b) Đường trung trực của đoạn thẳng AB là .............................
Bài 2: Trong các khẳng định sau khẳng định nào đúng, khẳng định nào sai
a) Hai đường thẳng vuông góc thì cắt nhau
b) Hai đường thẳng cắt nhau thì vuông góc
c) Đường thẳng xx' và yy' cắt nhau tạo thành 4 góc vuông
d) Khi 2 đường thẳng xx' và yy' vuông góc với nhau thì mỗi đường thẳng là đường phân giác của 1 góc bẹt.
Bài 3: Cho AB= 6cm. Hãy vẽ đường trung thực của đoạn thẳng AB, nêu cách vẽ.
Bài 4: Vẽ hình theo cách diễn đạt sau:
Vẽ góc xOy có số đo bằng 600. Lấy điểm A bất kì nằm trong góc xOy. Vẽ qua A đường thẳng d1 vuông góc với tia Ox tại B. Vẽ qua A đường thẳng d2 vuông góc với Oy tại C.
Bài 5: Cho đường thẳng d và điểm O nằm ngoài đường thẳng d. Chỉ sử dụng eke hãy vẽ đường thẳng d' đi qua O và vuông góc với d. Nói rõ cách vẽ
Bài 6: vẽ MN= 3cm, NP= 4cm. Hãy vẽ đường trung trực của mỗi đoạn thẳng ấy. Nêu cách vẽ
Bài 7: Trên cùng một nửa mặt phẳng có bờ chứa tia OA, vẽ các tia OB, OC sao cho AOB = 700 , OC vuông góc với OA. Tính số đo góc BOC
Câu hỏi tương tự Đọc thêm
a, ...cắt nhau và trong số các góc tạo thành có một góc bằng 90°
b, ...một...
c, ...là đường thẳng vuông góc với AB tại trung điểm M của đoạn thẳng AB

Giải
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ + ˆxOy′xOy′^)
mà (ˆxOyxOy^ + ˆxOy′xOy′^) = 1800 (2 góc kề bù)
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 12121800 = 900
Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông
b) Nếu M thuộc Ot hoặc Ot' thì M cách đều hai đường thẳng xx' và yy'
Thật vậy: M ε Ot do Ot là phân giác của ˆxOyxOy^ nên M cách đều Ox, Oy
=> M cách đều xx',yy'
M ε Ot'do Ot' là phân giác của ˆxOy′xOy′^ nên M cách đều xx', yy'
=> M cách đều xx',yy'
c) M cách đều hai đường thẳng xx', yy'
Nếu M nằm trong một góc trong bốn góc ˆxOyxOy^, ˆxOy′xOy′^, ˆx′Oy′x′Oy′^, ˆx′Oyx′Oy^ thì M phải thuộc phân giác của góc ây tức M phải thuộc Ot hoặc Ot'
d) Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0
e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo bởi hai đường thẳng cắt nhau đó.
a) Vì Ot là phân giác của ˆxOyxOy^
nên ˆyOtyOt^ = ˆxOtxOt^ = 1212ˆxOyxOy^
Ot' là phân giác của ˆxOy′xOy′^
nên ˆxOt′xOt′^ = ˆy′Ot′y′Ot′^ = 1212ˆxOy′xOy′^
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212ˆxOyxOy^ + 1212ˆxOy′xOy′^ = 1212(ˆxOyxOy^ + ˆxOy′xOy′^)
mà (ˆxOyxOy^ + ˆxOy′xOy′^) = 180
0
(2 góc kề bù)
=> ˆxOtxOt^ + ˆxOt′xOt′^ = 1212180
0 = 90
0
Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông
b) Nếu M thuộc Ot hoặc Ot' thì M cách đều hai đường thẳng xx' và yy'
Thật vậy: M ε Ot do Ot là phân giác của ˆxOyxOy^ nên M cách đều Ox, Oy
=> M cách đều xx',yy'
M ε Ot'do Ot' là phân giác của ˆxOy′xOy′^ nên M cách đều xx', yy'
=> M cách đều xx',yy'
c) M cách đều hai đường thẳng xx', yy'
Nếu M nằm trong một góc trong bốn góc ˆxOyxOy^, ˆxOy′xOy′^, ˆx′Oy′x′Oy′^, ˆx′Oyx′Oy^ thì M phải thuộc phân giác của góc ây tức M phải thuộc Ot hoặc Ot'
d) Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0
e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo
bởi hai đường thẳng cắt nhau đó.

a) Đúng
b) Đúng
c) Đúng
có phải là 3 ko