Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

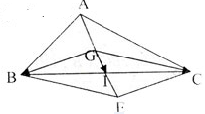
a) Ta có: \(\overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} \)\( = 4\overrightarrow {EG} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \)
Mà: \(\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM} ;\) (do M là trung điểm của AB)
\(\overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GN} \) (do N là trung điểm của CD)
\( \Rightarrow \overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = 4\overrightarrow {EG} + 2(\overrightarrow {GM} + \overrightarrow {GN} ) = 4\overrightarrow {EG} \) (do G là trung điểm của MN)
b) Vì E là trọng tâm tam giác BCD nên \(\overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = \overrightarrow 0 \)
Từ ý a ta suy ra \(\overrightarrow {EA} = 4\overrightarrow {EG} \)
c) Ta có: \(\overrightarrow {EA} = 4\overrightarrow {EG} \Leftrightarrow \overrightarrow {EA} = 4.(\overrightarrow {EA} + \overrightarrow {AG} ) \Leftrightarrow - 3\overrightarrow {EA} = 4\overrightarrow {AG} \)
\( \Leftrightarrow 3\overrightarrow {AE} = 4\overrightarrow {AG} \) hay \(\overrightarrow {AG} = \frac{3}{4}\overrightarrow {AE} \)
Suy ra A, G, E thẳng hàng và \(AG = \frac{3}{4}AE \) nên G thuộc đoạn AE.

a: \(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AI}+\overrightarrow{IB}+\overrightarrow{DI}+\overrightarrow{IC}\)
\(=\overrightarrow{AI}+\overrightarrow{DI}=-\left(\overrightarrow{IA}+\overrightarrow{ID}\right)=-2\overrightarrow{IM}=2\overrightarrow{MI}\)
\(\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AC}+\overrightarrow{DB}\)
\(\Leftrightarrow\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{DB}-\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{CA}+\overrightarrow{AB}=\overrightarrow{CD}+\overrightarrow{DB}=\overrightarrow{CB}\)(luôn đúng)
=>ĐPCM
b: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}\)
\(=2\cdot\overrightarrow{GM}+2\cdot\overrightarrow{GI}=\overrightarrow{0}\)

Ta có:
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \Leftrightarrow \left( {\overrightarrow {GI} + \overrightarrow {IA} } \right) + \left( {\overrightarrow {GI} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JC} } \right) + \left( {\overrightarrow {GJ} + \overrightarrow {JD} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {GI} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) + 2\overrightarrow {GJ} + \left( {\overrightarrow {JC} + \overrightarrow {JD} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {GI} + 2\overrightarrow {GJ} = \overrightarrow 0 \Leftrightarrow 2\left( {\overrightarrow {GI} + \overrightarrow {GJ} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {GI} + \overrightarrow {GJ} = \overrightarrow 0 \Rightarrow \)G là trung điểm của đoạn thẳng IJ
Vậy I, G, J thẳng hàng

Kéo dài AG lấy E sao cho AG=GE
\(2\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GB}=\overrightarrow{GE}+\overrightarrow{GB}=\overrightarrow{AG}+\overrightarrow{GB}=\overrightarrow{AB}\)
\(\overrightarrow{GI}=\overrightarrow{IA}\Rightarrow6\overrightarrow{GI}=3\overrightarrow{GA}\)
\(\overrightarrow{AB}+\overrightarrow{AC}+3\overrightarrow{GA}=\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GA}=\overrightarrow{GE}+\overrightarrow{GA}=\overrightarrow{AG}+\overrightarrow{GA}=\overrightarrow{0}\)