Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có:\(AE=EB=\frac{1}{2}AB\)
\(\text{AF}=FC=\frac{1}{2}CD\)
mà AB=CD( 2 cạnh đối trong hìh bình hành
=> AE=EB=AF=FC
Ta có: Tứ giác AFCE có : AE=FC(cmt)
AE//FC
=> AFCE là hình bình hành
Tứ giác BEDF có : EB=FD(cmt)
EB//FD
=> BEDF là hình bình hành
b)Ta có: AECF là hình bình hành
=> AF//CE và AF=CE
BEDF là hình bình hành
=> BF//DE và BF=DE

a) ta có: AB=DC ( vì ABCD là hình bình hành)
=> AE=FC (1)
lại có AB// CD( vì ABCD là hình bình hành) => AE// FC (2)
Từ (1) và (2) suy ra AECF là hình bình hành (dhnb)
CM tương tự ta được EBFD là hình bình hành
b) ta có AF // CE và AF = CE ( vì AFCE là hình bình hành )
lại có BF // DE và BF = DE ( vì BEDF là hình bình hành)

mình rất muốn nhưng mình không biết
mình là trần thị lâm hiền ở onlinemath đây mà

Xét tam giác ADM và tam giác CBN có:
AD = CN (ABCD là hình bình hành)
ADM = CBN (2 góc so le trong, AB // CB)
DM = BN (gt)
=> Tam giác ADM = Tam giác CBN (c.g.c)
=> AM = CN (2 cạnh tương ứng)
AMD = CNB (2 góc tương ứng) => 1800 - AMD = 1800 - CNB => AMN = CNM mà 2 góc này ở vị trí so le trong => AM // CN
=> AMCN là hình bình hành
=> AMCN là hình thoi
<=> AC _I_ BD
<=> ABCD là hình thoi

1.a) Ta có : góc MAN= GÓC MCN \(\Rightarrow\)NC // AM (1)
Lại có ABCD là hình bình hành \(\Rightarrow\) AB//=DC (2)
từ (1) và (2) \(\Rightarrow\) ANCM là hình bình hành( tứ giác có 2 cặp cạnh // với nhau)
2)
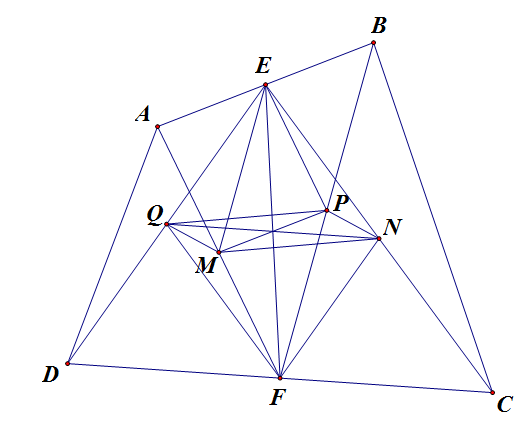
Sử dụng tính chất đường trung bình. Dễ dàng chứng minh QENF,MEPFQENF,MEPF là hình bình hành
Vậy EFEF và QNQN giao nhau tại trung điểm mỗi đường, EFEF và MPMP giao nhau tại trung điểm mỗi đường.
⇒QN⇒QN giao MPMP tại trung điểm mỗi đường.
Vậy QPNMQPNM là hình bình hành.

a) Xét tam giác ABD có:
AD = AB (giả thiết)
=> Tam giác ABD là tam giác cân
=> Góc B = góc D (t/chất của tam giác cân)
Có: Q là tr/điểm AD
M là tr/điểm AB
=> QM // BD (t/chất đg tr/bình của tam giác)
=>Tứ giác QMBD là hình thang
Mà: Góc B = góc D (tam giác ABD là tam giác cân)
=> Hình thang QMBD là hình thang cân
P/s: Mình giải đến đây thôi. Mình thấy câu b "có j đó sai sai"?! Chẳng phải ở trên đã nói M là tr/điểm của AB rồi sao?! Sao ở câu b lại nói I là tr/điểm của AB?! Mình chưa giải câu c vì mik nghĩ đáp án câu b có thế sẽ là manh mối để giải câu c. Mình mong nếu bạn viết nhầm thì mau mau sửa lại để mik giải tiếp!!!! Thân.![]()

A B C I H K F E a) Theo gt ta có :
FD // AC => FD // AE ( E \(\in AC\)) ( 1)
DE // AB => DE // AF ( F \(\in AB\) ) (2)
từ (1)(2) \(\Rightarrow AEDF\) là hình bình hành ( theo dấu hiệu nhận biết hình bình 1)
b)
theo a) tao có AEDF là hình bình hành
hình bình hành có 2 đường chéo AD và EF giao nhau tại I
=> I là trung điểm của 2 đường chéo AD và EF ( t/c hình bình hành )
=> \(IF=IE\) hay F đối xứng với E qua I
a)Xét tứ giác AEDF có: DE//AB, DF//AC
\(\Rightarrow\)AEDE là hình bình hành
b) Vì 2 đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường nên IA=ID, IF=IE suy ra E đối xứng với F qua I

A B C D A' C' B' E O F O'
Kí hiệu các điểm như hình vẽ.
Dễ dàng chứng minh được tam giác O'FO = tam giác O'C'C
=> OF = CC' (1) và OO' = O'C = 1/2OC => OO' = 1/3AO'
ta có OF là đường trung bình của tam giác BDB' vì \(\begin{cases}OB=OD\\FO\text{//}BB'\end{cases}\)
=> BB' = 2OF (2)
Từ (1) và (2) suy ra được BB'+CC' = 3OF (*)
Mặt khác, vì OF // AA' nên áp dụng định lí Talet ta có :
\(\frac{OF}{AA'}=\frac{OO'}{AO'}=\frac{1}{3}\Rightarrow AA'=3OF\) (**)
Từ (*) và (**) ta suy ra đpcm.
AE = EB = AB/2 (E là trung điểm của AB)
CF = FD = CD/2 (F là trung điểm của CD)
mà AB = CD (ABCD là hbh)
=> AE = CF
mà AE // CF (AB // CD, E thuộc AB, F thuộc CD)
=> AECF là hbh.