Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có:\(AE=EB=\frac{1}{2}AB\)
\(\text{AF}=FC=\frac{1}{2}CD\)
mà AB=CD( 2 cạnh đối trong hìh bình hành
=> AE=EB=AF=FC
Ta có: Tứ giác AFCE có : AE=FC(cmt)
AE//FC
=> AFCE là hình bình hành
Tứ giác BEDF có : EB=FD(cmt)
EB//FD
=> BEDF là hình bình hành
b)Ta có: AECF là hình bình hành
=> AF//CE và AF=CE
BEDF là hình bình hành
=> BF//DE và BF=DE

a.
Xet 2 tam giac ADE va CBF ta co:
\(\widehat{A}=\widehat{C}\)(2 goc doi cua hinh binh hanh)
\(AE=CF\)
\(AD=BC\)(2 canh doi cua hinh binh hanh)
Do do:\(\Delta ADE=\Delta CBF\left(c-g-c\right)\)
Suy ra:\(DE=BF\)(2 canh tuong ung)
b.Xet 2 tam giac ADF va CBE ta co:
\(\widehat{D}=\widehat{B}\)(2 goc doi cua hinh binh hanh)
\(DF=BE\)
\(AD=CB\)(2 canh doi cua hinh binh hanh)
Do do:\(\Delta ADF=\Delta CBE\left(c-g-c\right)\)
Suy ra:\(AF=CE\)(2 canh tuong ung)
Tu giac AECF co:
\(AE=CF\)
\(AF=CE\)
Nen AECF la hinh binh hanh
Suy ra:\(\widehat{BAF}=\widehat{DCE}\)(2 goc doi cua hinh binh hanh)
Theo chung minh o cau a ta co:\(\Delta ADE=\Delta CBF\)
Suy ra:\(\widehat{AED}=\widehat{CFB}\)(2 goc tuong ung)
Xet 2 tam giac EAM va FCN ta co:
\(AE=CF\)
\(\widehat{BAF}=\widehat{DCE}\)
\(\widehat{AED}=\widehat{CFB}\)
Do do:\(\Delta EAM=\Delta FCN\left(g-c-g\right)\)
Suy ra:\(EM=FN\left(1\right)\)(2 canh tuong ung)
Va \(\widehat{AME}=\widehat{CNF}\)(2 goc tuong ung)
Ma \(\widehat{DMF}=\widehat{AME}\left(2\right)\)
\(\widehat{BNE}=\widehat{CNF}\left(3\right)\)
Tu (2) va (3) suy ra:\(\widehat{DMF}=\widehat{BNE}\)
Tu giac EBFD co:
\(BE=DF\)
\(DE=BF\)(chung minh o cau a)
Nen EBFD la hinh binh hanh
Suy ra;\(\widehat{EDF}=\widehat{FBE}\)(2 goc doi cua hinh binh hanh)
Xet 2 tam giac DMF va BNE ta co:
\(\widehat{DMF}=\widehat{BNE}\)
\(\widehat{EDF}=\widehat{FBE}\)
\(DF=BE\)
Do do:\(\Delta DMF=\Delta BNE\left(c-g-c\right)\)
Suy ra;\(MF=NE\left(4\right)\)(2 canh tuong ung)
Tu (1) va (4) suy ra:EMFN la hinh binh hanh

làm đc mỗi câu b :))
AEFC là hình bình hành ( tự cm nhá :) )
=> đường chéo AC giao đường chéo EF tại trung điểm của EF
câu a => đường chéo MN giao đường chéo EF tại trung điểm của EF
=> ĐPCM
câu b thui, câu a lằng nhằng quá lười nghĩ thông cảm nhé

b tham khảo nha
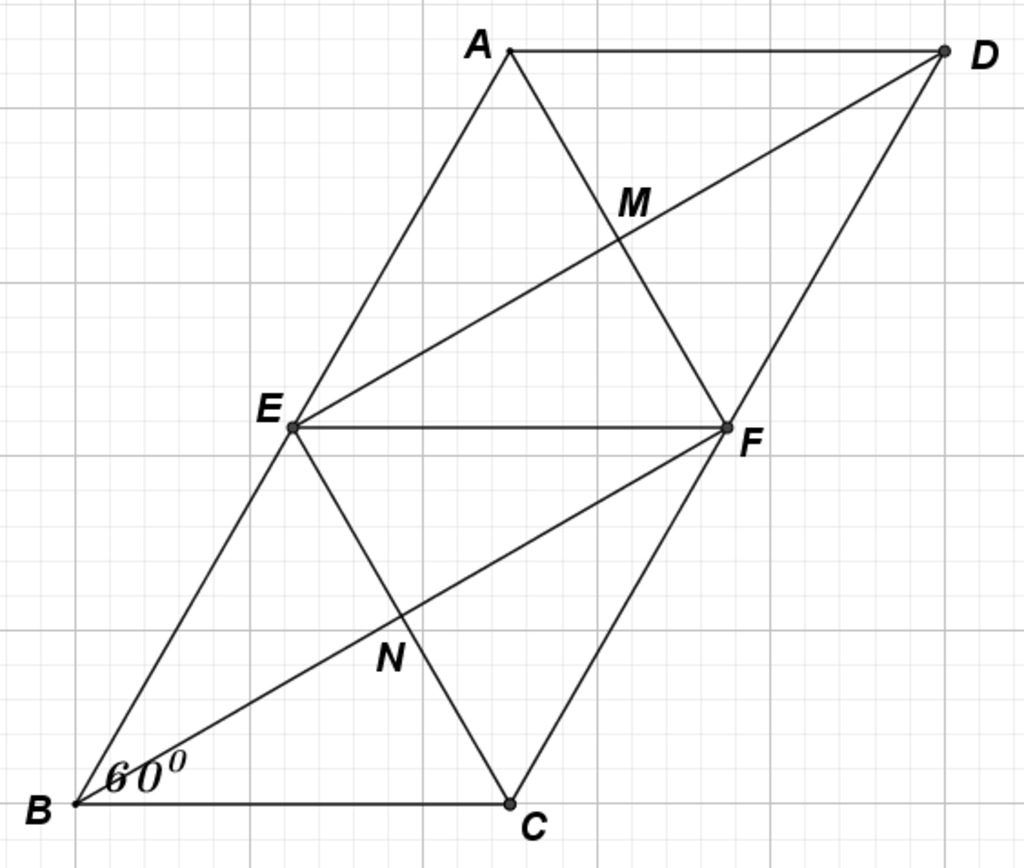
a) Do ABCD là hình bình hành nên AB= CD và AB//CD
Và E và F là trung điểm của AB và CD => AE=BE=CF=DF và BE//DF
Xét tứ giác DEBF có : BE//DF và BE=DF=> DEBF là hình bình hành
b)
Xét AEDF có AE//DF và AE=DF=> AEDF là hình bình hành
Lại có: CD= 2BC= 2 AD nên AD= AE (=1/2 CD)
=> hình bình hành AEDF là hình thoi
c)ta cm được AECF là hình bình hành và M, N là trung điểm của AF và CE
=> MF= EN và MF//EN=> EMFN là hình bình hành
Lại có AEDF là hình thoi nên AN⊥DE tại M
=> góc EMF vuông=> hình bình hành EMFN là hình chữ nhật
d) Chứng minh được
SAFB=12SABCDSBEC=14SABCDˆB=600⇒ΔBECdeucanh=AB2=2(cm)⇒SBEC=√3(cm2)⇒SAFB
bạn vẽ hình nhé mình chứng minh lun
a) ta có: AB=DC ( vì ABCD là hình bình hành)
=> AE=FC (1)
lại có AB// CD( vì ABCD là hình bình hành) => AE// FC (2)
Từ (1) và (2) suy ra AECF là hình bình hành (dhnb)
CM tương tự ta được EBFD là hình bình hành
b) ta có AF // CE và AF = CE ( vì AFCE là hình bình hành )
lại có BF // DE và BF = DE ( vì BEDF là hình bình hành)