Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
- Đường thẳng d’ song song với d nên có dạng: 3x+ y+ m= 0
- IH là khoảng cách từ I đến d’:
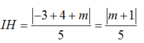
- Xét tam giác vuông IHB:

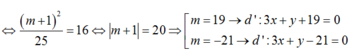

Đường tròn (C) tâm I(1;2) bán kính \(R=\sqrt{5}\)
a.
\(\overrightarrow{OI}=\left(1;2\right)\Rightarrow\) đường thẳng OI nhận (2;-1) là 1 vtpt
Phương trình: \(2\left(x-0\right)-1\left(y-0\right)=0\Leftrightarrow2x-y=0\)
b.
Gọi H là trung điểm AB \(\Rightarrow IH\perp AB\Rightarrow IH=d\left(I;\Delta\right)\)
Áp dụng định lý Pitago:
\(IH=\sqrt{IA^2-AH^2}=\sqrt{R^2-\left(\dfrac{AB}{2}\right)^2}=\dfrac{\sqrt{2}}{2}\)
Phương trình \(\Delta\) qua M có dạng:
\(a\left(x-1\right)+b\left(y-3\right)=0\) với \(a^2+b^2>0\)
\(d\left(I;\Delta\right)=\dfrac{\left|a\left(1-1\right)+b\left(2-3\right)\right|}{\sqrt{a^2+b^2}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left|\sqrt{2}b\right|=\sqrt{a^2+b^2}\Leftrightarrow2b^2=a^2+b^2\)
\(\Leftrightarrow a^2=b^2\Leftrightarrow\left[{}\begin{matrix}a=b\\a=-b\end{matrix}\right.\)
Chọn \(a=1\Rightarrow\left[{}\begin{matrix}\left(a;b\right)=\left(1;1\right)\\\left(a;b\right)=\left(1;-1\right)\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}1\left(x-1\right)+1\left(y-3\right)=0\\1\left(x-1\right)-1\left(y-3\right)=0\end{matrix}\right.\)

\(d\left(I;\left(d\right)\right)=\dfrac{\left|3\cdot\left(-1\right)+2\cdot\left(-1\right)-15\right|}{\sqrt{3^2+1}}=2\sqrt{10}\)
\(R=\sqrt{\left(2\sqrt{10}\right)^2+\left(\dfrac{6}{2}\right)^2}=7\)
=>(x+1)^2+(y-2)^2=49

Đáp án A
- Từ giả thiết : đường tròn (C1) tâm I(0;0); R = 13 đường tròn (C2) tâm J( 6;0) và R’= 5
- Gọi đường thẳng d qua A có véc tơ chỉ phương:

- d cắt (C1) tại A,B:
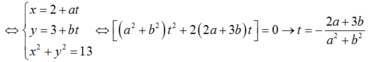
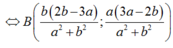
Tương tự d cắt (C2) tại A; C thì tọa độ của A; C là nghiệm của hệ :
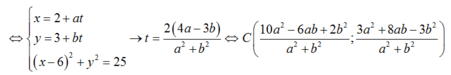
- Nếu 2 dây cung bằng nhau thì A là trung điểm của A; C .Từ đó ta có phương trình :
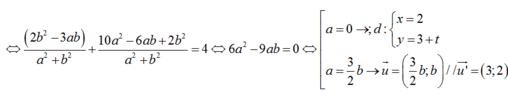
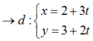
Vậy có 2 đường thẳng: d: x-2 = 0 và d’: 2x -3y + 5= 0.

(C): x^2+y^2-4x+6y-12=0
=>O(2;-3)
R=căn 2^2+(-3)^2+12=5
Gọi đường cần tìm là (d'): x+y+c=0
Gọi A,B lần lượt là giao điểm của (d') và (C)
ΔOHB vuông tại H
\(d\left(O;AB\right)=\dfrac{\left|2+\left(-3\right)+c\right|}{\sqrt{2}}=HO\)
\(=\sqrt{OB^2-BH^2}=3\)
=>\(\left[{}\begin{matrix}c=3\sqrt{2}+1\\c=-3\sqrt{2}+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x+y-3\sqrt{2}+1=0\\x+y+3\sqrt{2}+1=0\end{matrix}\right.\)

a) Để tìm tọa độ tâm và bán kính của đường tròn ©, ta cần viết lại phương trình của nó dưới dạng chuẩn:
\begin{align*}
x^2 + y^2 - 2x + 6y - 2 &= 0 \
\Leftrightarrow (x-1)^2 + (y+3)^2 &= 14
\end{align*}
Vậy, tọa độ tâm của đường tròn © là $(1,-3)$ và bán kính của đường tròn © là $\sqrt{14}$.
b) Đường tròn có tâm $I(4,3)$ và đi qua $A(-4,1)$ có phương trình là:
$$(x-4)^2 + (y-3)^2 = (-4-4)^2 + (1-3)^2 = 20$$
c) Để tìm phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d: 3x+4y-4=0$ tại hai điểm $M$ và $N$ sao cho $MN=6$, ta có thể làm như sau:
Tìm giao điểm $H$ của đường thẳng $d$ và đường vuông góc với $d$ đi qua $I$.Tìm hai điểm $M$ và $N$ trên đường thẳng $d$ sao cho $HM=HN=3$.Xây dựng đường tròn (C') có tâm là $I$ và bán kính bằng $IN=IM=\sqrt{3^2+4^2}=5$.
Để tìm giao điểm $H$, ta cần tìm phương trình của đường thẳng vuông góc với $d$ đi qua $I$. Đường thẳng đó có phương trình là:
$$4x - 3y - 7 = 0$$
Giao điểm $H$ của đường thẳng này và $d$ có tọa độ là $(\frac{52}{25}, \frac{9}{25})$.
Để tìm hai điểm $M$ và $N$, ta có thể sử dụng công thức khoảng cách giữa điểm và đường thẳng. Khoảng cách từ điểm $H$ đến đường thẳng $d$ là:
$$d(H,d) = \frac{|3\cdot \frac{52}{25} + 4\cdot \frac{9}{25} - 4|}{\sqrt{3^2+4^2}} = \frac{1}{5}$$
Vậy, hai điểm $M$ và $N$ cách $H$ một khoảng bằng $\frac{3}{5}$ và $\frac{4}{5}$ đơn vị theo hướng vuông góc với $d$. Ta có thể tính được tọa độ của $M$ và $N$ như sau:
$$M = \left(\frac{52}{25} - \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{3}{5}\cdot 3\right) = \left(\frac{12}{25}, \frac{54}{25}\right)$$
và
$$N = \left(\frac{52}{25} + \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{4}{5}\cdot 3\right) = \left(\frac{92}{25}, \frac{27}{5}\right)$$
Cuối cùng, phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d$ tại hai điểm $M$ và $N$ sao cho $MN=6$ là:
$$(x-4)^2 + (y-3)^2 = 5^2$$

M N I (d) H
gọi M,N là hai điểm cắt đg tròn tâm I
kẻ IH vuông góc với MN ,theo đề bài ta có MN =6 => MH=3
độ dài từ tâm I đến (d) =\(\dfrac{\left|2.3-5.-1+18\right|}{\sqrt{2^2+\left(-5\right)^2}}=\sqrt{29}\)
Áp dụng pytago vào tam giác vuông IMH ta có
\(IM=\sqrt{IH^2+MH^2}=\sqrt{38}\)
vậy pt đg tròn là \(\left(x-3\right)^2+\left(y+1\right)^2=\left(\sqrt{38}\right)^2\)( tới đây bạn tự khai triển ra nha
b ) cách làm tương tự
2 .
I N M H P
MN max khi nó là đường kính > nó phải đi qua điểm I
\(\overrightarrow{uIA}=\left(4;-2\right)=>n\overrightarrow{IA}=\left(2;4\right)\)
ptđt \(\Delta:2\left(x-3\right)+4\left(y-0\right)=0\)
MN min
ta có MN=2HM
trg tam giác vuông IHMtheo pytago ta có \(HM=\sqrt{IA^2-IH^2}\)có IA là bán kính ( cố định ) => IH max thì MN min
lại xét tam giác IHP trong tam giác IHP thì có IP là cạch huyền mà trg tam giác cạc huyền là cạch lớn nhất nên IH max khi điểm H trùng với điểm P .
vậy toạ độ A trùng với P nên \(u\overrightarrow{IP}=\left(4;-2\right)=n\overrightarrow{\Delta}\)
ptđt là \(4\left(x-3\right)-2\left(y-0\right)=0\)
mình trình bày hơi tệ bạn thông cảm nha !