Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do các tấm thẻ giống nhau, nên lấy 3 tấm từ 10 tấm không quan tâm thứ tự có \(C_{10}^3 = 120\)cách, suy ra \(n\left( \Omega \right) = 120\)
Gọi A là biến cố “Tích các số ghi trên ba thẻ đó là số chẵn”
Để tích các số trên thẻ là số chẵn thì ít nhất có 1 thẻ là số chẵn
Để chọn ra 3 thẻ thuận lợi cho biến cố A ta có 3 khả năng
+) Khả năng 1: 3 thẻ chọn ra có 1 thẻ có số chẵn và 2 thẻ có số lẻ có \(5.C_5^2 = 50\) khả năng
+) Khả năng 2: 3 thẻ chọn ra có 2 thẻ có số chẵn và 1 thẻ có số lẻ có \(C_5^2.5 = 50\) khả năng
+) Khả năng 3: 3 thẻ chọn ra có đều là có số chắn có \(C_5^3 = 10\) khả năng
Suy ra \(n\left( A \right) = 50 + 50 + 10 = 110\)
Vậy xác suất của biến cố A là: \(P(A) = \frac{{110}}{{120}} = \frac{{11}}{{12}}\)

a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 2 của 20 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_{20}^2\) ( phần tử)
b) Gọi A là biến cố “Tích các số trên hai thẻ là số lẻ”
Để tích các số trên thẻ là số lẻ thì cả hai thẻ bốc được đểu phải là số lẻ vậy nên ta phải chọn ngẫu nhiên 2 thẻ từ 10 thẻ số lẻ. Do đó, số phần tử các kết quả thuận lợi cho biến cố A là tổ hợp chập 2 của 10 phần tử: \(n\left( A \right) = C_{10}^2\) ( phần tử)
Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{10}^2}}{{C_{20}^2}} = \frac{9}{{38}}\)

Ta có \(n\left( \Omega \right) = C_{11}^2 = 55\).
a) Có 5 số lẻ là \(\left\{ {11;13;15;17;19} \right\}\) nên \(n\left( C \right) = C_5^2 = 10\). Vậy \(P\left( C \right) = \frac{{10}}{{55}} = \frac{2}{{11}}\).
b) Có 6 số chẵn là \(\left\{ {10;12;14;16;18;20} \right\}\) nên \(n\left( D \right) = C_6^2 = 15\). Vậy \(P\left( D \right) = \frac{{15}}{{55}} = \frac{3}{{11}}\).

a) Kí hiệu \({X_1},{X_2},...,{X_7}\) là bảy thẻ màu xanh, \({D_1},{D_2},...,{D_5}\) là 5 thẻ màu đỏ và \({V_1},{V_2}\) là hai thẻ màu vàng.
Ta có không gian mẫu là \(\Omega = \left\{ {{X_1},{X_2},...,{X_7},{D_1},{D_2},...,{D_5},{V_1},{V_2}} \right\}\).
b) Ta có \(A = \left\{ {{D_1},{D_2},{D_3},{D_4},{D_5},{V_1},{V_2}} \right\},B = \left\{ {{X_2},{X_3},{D_2},{D_3},{V_2}} \right\}\).

Số phần tử của không gian mẫu là \(n\left( \Omega \right) = 5.5 = 25\).
Gọi E là biến cố: “thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I”
\(E = \left\{ {\left( {4,5} \right);\left( {3,4} \right);\left( {3,5} \right);\left( {2,3} \right);\left( {2,4} \right);\left( {2,5} \right);\left( {1,2} \right);\left( {1;3} \right);\left( {1,4} \right);\left( {1,5} \right)} \right\}\) suy ra \(n\left( E \right) = 10\)
Vậy \(P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega \right)}} = \frac{2}{5}\)

a) Lần đầu tiên lấy thẻ, sau đó để lại vào hộp nên lần thứ 2 cũng sẽ có 3 trường hợp với 3 số xảy ra, nên ta có không gian mẫu của phép thử là:
\(\Omega = \left\{ {\left( {i;j} \right)\left| {i,j = 1,2,3} \right.} \right\}\) với i, j lần lượt là số được đánh trên thẻ được lấy lần đầu và lần hai
b) Lần đầu lấy một thẻ từ hộp, xem số, bỏ ra ngoài rồi lấy tiếp 1 thẻ khác từ hộp, nên lần hai chỉ có 2 trường hợp với hai số còn lại, nên ta có không gian mẫu của phép thử là:
\(\Omega = \left\{ {(1;2),(1;3),(2;1),(2;3),(3;1),(3;2)} \right\}\)
(Với kết quả của phép thử là cặp số (i; j) trong đó i và j lần lượt là số được đánh trên thẻ được lấy ra lần thứ nhất và thứ hai)
c) Ta lấy đồng thời hai thẻ nên các số được đánh trên thẻ là khác nhau
\(\Omega = \left\{ {(1;2),(1;3),(2;1),(2;3),(3;1),(3;2)} \right\}\)
(Với kết quả của phép thử là cặp số (i; j) trong đó i và j lần lượt là số được đánh trên thẻ được lấy ra lần thứ nhất và thứ hai)

a) Các kết quả có thể xảy ra trong 2 lần lấy tấm thẻ từ 2 hộp được thể hiện ở sơ đồ hình cây như hình dưới đây:
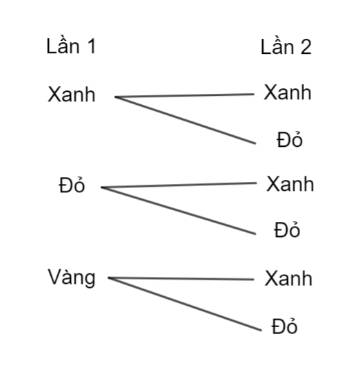
b)
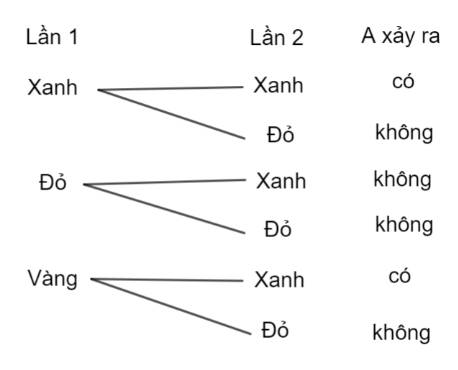
Gọi A là biến cố “Trong 2 thẻ lấy ra không có thẻ màu đỏ nào” là biến cố đối của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”
Dựa vào sơ đồ hình cây ta thấy có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho I. Do đó: \(P(A) = \frac{2}{6} = \frac{1}{3}\)
Vậy xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ” là \(1 - \frac{1}{3} = \frac{2}{3}\)

Tham khảo:
a) Vẽ sơ đồ cây ba tầng.
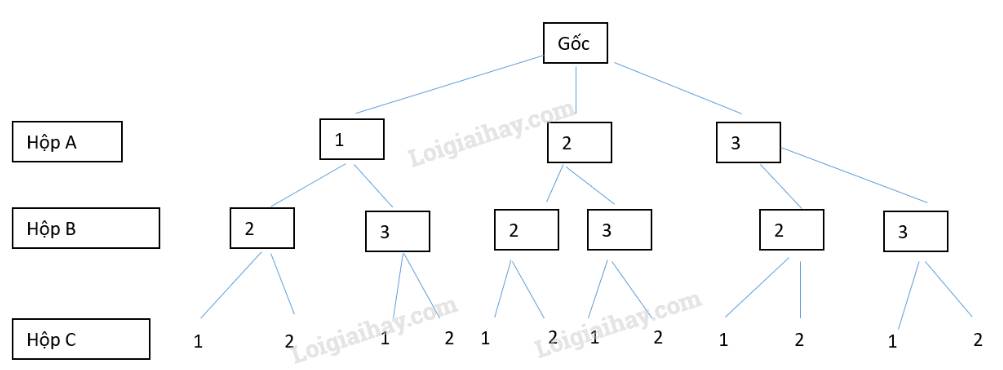
b) Chuyển qua biến cố đối: Từ sơ đồ cây xác định không gian mẫu và biến cố \(\overline M \): “Trong ba thẻ rút ra không có thẻ số 1”.
\(\begin{array}{l}\overline M = \left\{ {222;232;322;332} \right\}\\c, n(\overline M ) = 4\\P(\overline M ) = \frac{{n(\overline M )}}{{n(\Omega )}} = \frac{4}{{12}} = \frac{1}{3}\\ \Rightarrow P(M) = 1 - P(\overline M ) = 1 - \frac{1}{3} = \frac{2}{3}\end{array}\)
Gọi A là biến cố “Không bạn nào lấy đúng thẻ của mình”
Các kết quả có thể xảy ra khi các bạn lần lượt lấy thẻ được thể hiện ở sơ đồ hình cây như hình dưới
Có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho A, do đó:
\(P\left( A \right) = \frac{2}{6} = \frac{1}{3}\)