Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm
A = 1 giờ 24 phút + 1,4 giờ x 7 + 2 giờ 10 phút + 38 phút
A = 1,4 giờ + 1,4 giờ x 7 + 2 giờ 48 phút
A = 1,4 giờ + 1,4 giờ x 7 + 2,8 giờ
A = 1,4 giờ + 1,4 giờ x 7 + 1,4 giờ + 1,4 giờ
A = 1,4 giờ x ( 1 + 7 + 1 + 1 )
A = 1,4 giờ x 10
A = 14 giờ
Giải
1,4 giờ = 1 giờ 24 phút.
vậy ta có 1 giờ 24 phút + 1 giờ 24 phút x 7
= 1 giờ 24 phút x ( 7 + 1 )
= 1 giờ 24 phút x 8 2 giờ 10 phút + 38 phút
= 2 giờ 48 phút = 2 x 1 giờ 24 phút.
vậy ta có 1 giờ 24 phút x (8 + 2)
= 1 giờ 24 phút x 10 và 1 giờ 24 phút x 10
= 10 giờ 240 phút
= 14 giờ

a/ \(-12\left(x-5\right)+7\left(3-x\right)=5\)
\(< =>-12x+60+21-7x=5\)
\(< =>-19x+81=5\)
\(< =>-19x=-76\)
\(< =>x=\frac{76}{19}\)
b/ 30(x+2)-6(x-5)-24x=100
<=>30x + 60 - 6x + 30 - 24x =100
<=> 90=100( vô lý)
c/ \(\left(x-1\right)\left(x^2+1\right)=0\)
\(< =>\hept{\begin{cases}x-1=0\\x^2+1=0\end{cases}}< =>\hept{\begin{cases}x=1\\x^2=-1\left(voly\right)\end{cases}}\)
d/ làm rồi mà
a. \(-12.\left(x-5\right)+7.\left(3-x\right)=5\)
\(-12x+60+21-7x=5\)
\(-19x+81=5\)
\(-19x=-76\)
\(x=4\)
b. \(30.\left(x+2\right)-6.\left(x-5\right)-24x=100\)
\(30x+60-6x+30-24x=100\)
\(\left(30x-6x-24x\right)+\left(60+30\right)=100\)
\(90=100\)(vô lí)
\(\Rightarrow x=\varnothing\)
c. \(\left(x-1\right)\left(x^2+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\x^2+1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=1\\x^2=-1\left(loại\right)\end{cases}}}\)
\(\Rightarrow x=1\)
Câu d) chính là câu a) :D

Viết phương trình về dạng
\(\frac{2^x}{3^x+4^x}-\frac{4^x}{9^x+16^x}=\frac{-5}{2x}\) hay \(\frac{2^x}{3^x+4^x}+\frac{5}{x}=\frac{2^{2x}}{3^{2x}+4^{2x}}+\frac{5}{2x}\)
Xét hàm số \(f\left(t\right)=\frac{2^t}{3^t+4^t}+\frac{5}{t}\) luôn đồng biến
Đáp số : Phương trình vô nghiệm

Đáp án C
Gọi H là hình chiếu của M trên (P) => MH là khoảng cách từ M đến mặt phẳng (P). Đường thẳng D có vectơ chỉ phương u → =(2;1;3) mặt phẳng (P) có vectơ pháp tuyến n → =(1;1;-2)
Khi đó:
![]()
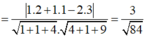
Tam giác MHA vuông tại H



a) 41,25 x 99 + 41,25
= 41,25 x 99 + 41,25 +1
= 41,25 x ( 99 + 1 )
= 41,25 x 100
= 4125

↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑ ↓ ↑

Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng
mơn a
a) 72 x 212 + 27 x 121 + 121
= 72 x 212 + 27 x 121 + 121
= 72 x 212 + 27 x 121 + 121 x 1
= 72 x 212 + (27 + 1) x 121
= 72 x 212 + 28 x 121
= 72 x (121 + 91) + 28 x 121
= 72 x 121 + 72 x 91 + 28 x 121
= (72 + 28) x 121 + 72 x 91
= 100 x 121 + 72 x 91
= 12100 + 6552
= 18652 (anh thấy bài này sao ý)
b) (165 x 99 + 165) - ( 163 x 101 - 163)
= (165 x 99 + 165 x 1) - ( 163 x 101 - 163 x 1)
= [165 x (99 + 1)] - [163 x (101 - 1)]
= 165 x 100 - 163 x 100
= 16500 - 16300
= 200
c) 24 x 62 + 48 x 19
= 24 x 62 + (24 + 24) x 19
= 24 x 62 + 24 x 19 + 24 x 19
= 24 x (62 + 19 + 19)
= 24 x 100
= 2400
d) 24 x 76 + 48 x 12 - 20 x 100
= 24 x 76 + (24 + 24) x 12 - 20 x 100
= 24 x 76 + 24 x 12 + 24 x 12 - 20 x 100
= 24 x (76 + 12 + 12) - 20 x 100
= 24 x 100 - 20 x 100
= 100 x (24 - 20)
= 100 x 4
= 400
( nhớ tính lại xem đúng ko nha, anh lỡ có sai thì chết. Bài nào sai báo ngay cho anh )
HỌC TỐT