Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài: Vẽ tam giác ABC biết ∠A = 900; AB = AC = 3cm. Sau đó đo các góc ∠B và ∠C.
Bài giải: Cách vẽ:
– Vẽ góc ∠xAy = 900
– Trên tia Ax vẽ đoạn thẳng AB = 3cm,
– Trên tia Ay vẽ đoạn thẳng AC = 3cm,
– Vẽ đoạn BC.
Ta vẽ được đoạn thẳng BC.
Ta đo các góc B và C ta được ∠B = ∠C = 450
Đề bài: Trên mỗi hình 82,83,84 sau có các tam giác nào bằng nhau? Vì sao?
Bài giải:
Hình 82:
∆ADB và ∆ADE có: AB = AE (gt)
∠A1b= ∠A2 , AD chung.
Nên ∆ADB = ∆ADE(c.g.c)
Hình 83:
∆HGK và ∆IKG có:
HG = IK (gt)
∠G = ∠K (gt)
GK là cạnh chung (gt)
nên ∆HGK = ∆IKG( c.g.c)
Hình 84:
∆PMQ và ∆PMN có: MP cạnh chung
∠M1 = ∠M2
Nhưng MN không bằng MQ. Nên PMQ không bằng PMN.

bn tự vẽ hình nha
ta có a+b+c=180(tổng 3 góc của tg) suy ra a+80+30=180 suy ra a=180-110=70 độ
ta có BAD=CAD=BAC/2(tia phân giác ad)
suy ra bad=cad=70/2=35 độ
ta có ADC=BAD+ABD=35+80=115(độ)
suy ra ADB=180-115=65 ĐỘ
CHỖ NÀO KO HIỂU THÌ HỎI MÌNH NHA BN HI HI
CHÚC BN HỌC TỐT

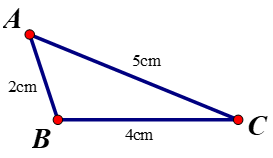
Dựa vào hình vẽ, ta có:
Góc đối diện cạnh BC là Â
Góc đối diện cạnh AC là B̂
Góc đối diện cạnh AB là Ĉ
Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.
2)heo định lý tổng ba góc trong tam giác ABC, ta có:
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Kiến thức áp dụng
+ Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
+ Định lý tổng ba góc trong tam giác: Trong một tam giác, tổng ba góc bằng 180º.
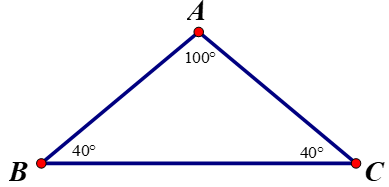
3 a) Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
b) Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có
4) Trong một tam giác ta luôn có:
+ Góc đối diện với cạnh lớn hơn là góc lớn hơn
⇒ góc đối diện với cạnh nhỏ nhất là góc nhỏ nhất.
+ Góc nhỏ nhất luôn là góc nhọn.
(Giả sử tồn tại tam giác có góc nhỏ nhất không phải góc nhọn
⇒ Góc nhỏ nhất ≥ 90º ⇒ cả ba góc ≥ 90º ⇒ tổng ba góc trong tam giác ≥ 90º.3 = 270º.
5) + Trong ∆BCD có góc C tù (gt) nên góc C lớn nhất ⇒ BD lớn nhất (vì BD là cạnh đối diện với góc C) ⇒ BD > CD (1).
+ Áp dụng định lý góc ngoài trong tam giác BCD ta có :
nên góc ABD cũng là góc tù.
Trong ∆ABD có góc B tù (cmt) nên góc B lớn nhất ⇒ AD lớn nhất (vì AD là cạnh đối diện với góc B) ⇒ AD > BD
(2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy Hạnh đi xa nhất, Trang đi gần nhất.
6)Vì D nằm giữa A và C (giả thiết)
⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)
⇒ AC > BC
Mà trong tam giác ABC :
Góc đối diện cạnh AC là góc B
Góc đối diện cạnh BC là góc A
Ta lại có: AC > BC (cmt)
⇒ B̂ > Â (theo định lí 1)
Hay  < B̂.
Vậy kết luận c) là đúng.
7)
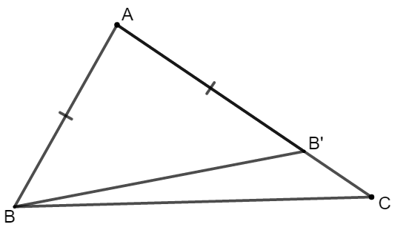
a) Trên tia AC, ta có : AC > AB mà AB = AB’ ⇒ AC > AB’ ⇒ B’ nằm giữa A và C.
⇒ tia B’B nằm giữa hai tia BA và BC.
b) ∆ABB’ có AB = AB’ nên ∆ABB’ cân tại A.
c) Vì góc AB'B là góc ngoài tại B’ của ∆BB’C

Bài 6:
A P M N Q 33 o
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).

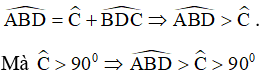
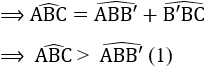
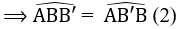
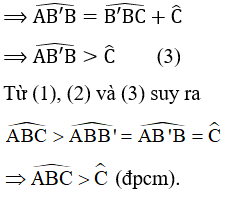
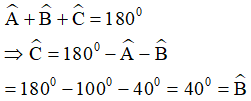
 giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
A X x, y y,
hai góc vuông ko đối đỉnh:xAy và xAy,
x,Ay và x,Ay,
(x+1)2=49=72=(-7)2
=>x+1=7,-7
=>x=6,-8
Vậy x=6,-8