Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


sgk toán 8 tập 1
Bài 74. Hai đường chéo của một hình thoi bằng 8cm8cm và 10cm10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
(A) 6cm6cm; (B) √41cm41cm
(C) √164cm164cm (D) 9cm9cm ?
Bài giải:
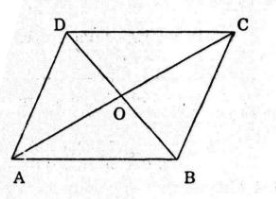
Xét bài toán tổng quát:
ABCDABCD là hình thoi, OO là giao điểm hai đường chéo.
Theo tính của hình thoi hai đường chéo của hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.
Áp dụng định lí Pytago vào tam giác vuông ABOABO ta có:
AB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=√(12AC)2+(12BD)2=√42+52=√41cmAB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=(12AC)2+(12BD)2=42+52=41cm
Vậy (B) đúng.
Bài 79.
a) Một hình vuông có cạnh bằng 3cm3cm. Đường chéo của hình vuông đó bằng 6cm6cm, √18cm18cm, 5cm5cm hay 4cm4cm ?
b) Đường chéo của một hình vuông bằng 2dm2dm. Cạnh cảu hình vuông đó bằng: 1dm1dm,
32dm32dm, √2dm2dm hay 43dm43dm ?
Bài giải:
a) Gọi đường chéo của hình vuông có độ dài là aa.
Ta có: a2=32+32=18a2=32+32=18
Suy ra a=√18a=18
Vậy đường chéo của hình vuông đó bằng √18cm18cm.
b) Gọi cạnh của hình vuông là aa.
Ta có a2+a2=22⇒2a2=4⇒a2=2⇒a=√2a2+a2=22⇒2a2=4⇒a2=2⇒a=2
Vậy cạnh của hình vuông đó bằng √2dm2dm.



Cậu nói thế thì ai biết?Phải đăng đầu bài lên chứ
tâm điểm là bn ấy lười đó Hà MY ak!!!!!!!!!!!!!!!!!