Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


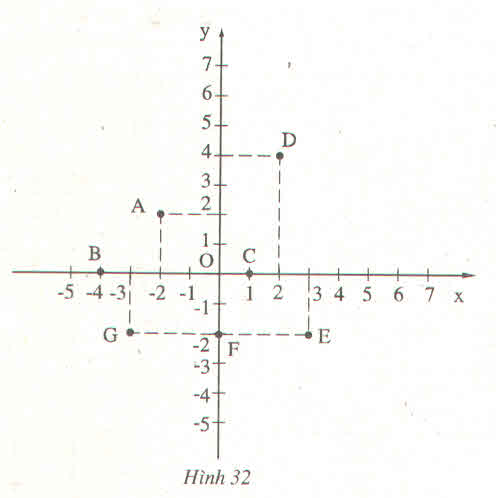
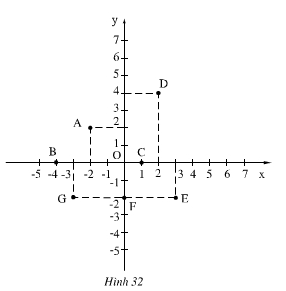
Ta có tọa độ các điểm: A(-2; 2); B(-4; 0); C(1; 0); D(2; 4); E(3; -2); F(0; -2); G(-3; -2)

A( -3; 3 )
B ( -1; 2 )
C ( -5; 0 )
M ( 2; 3 )
N ( 5; 3 )
Q ( 2; 1 )
P (5; 1 )

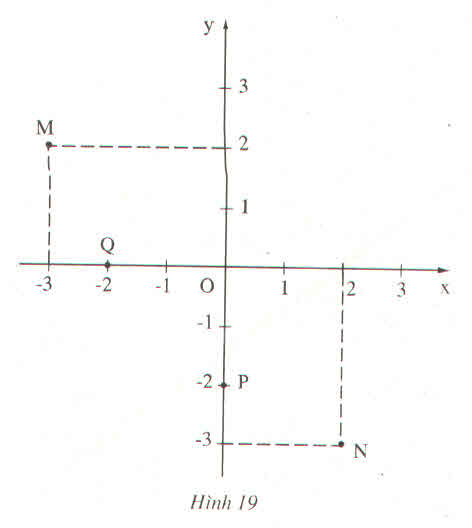
a) M(-3; 2); N(2; -3); Q(-2; 0); P(0; -2)
b) Ta thấy hoành độ của điểm M chính là tung độ của điểm N, và tung độ của M chính là hoành độ của N.
Bài 32.
a, M ( -3,2 ) ; N ( 2;-3 ) ; P ( 0,-2 ) ; Q ( -2,0 )
b, Nhận xét : + Hoành độ của M = Tung độ của N
+ Hoành độ của N = Tung độ của M
+ Hoành độ của P = Tung độcủa Q
+ Hoành độ của Q = Tung độ của P

a) Ta có:
M(2;3), N(3;2), P(0;-3), Q (-3;0).
b) Hoành độ điểm M là trung độ điểm N.
Tung độ điểm M là hoành độ điểm N.
Hoành độ điểm P là tung độ điểm Q, tung độ điểm P là hoành độ điểm Q.
a)M (2;3) , N( 3;2) , P( 0;-3), Q(-3;0)
b) Trong mỗi điểm: Hoành độ của điểm này bằng tung độ của điểm kia và ngươc lại

A (0,5; 2) B (2;2) C (2;0)
D (0,5; 0) P (-3;3) Q (-1;1)
R(-3;1)
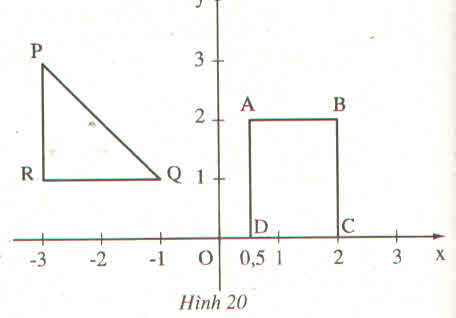
- A(0,5 ; 2); B(2 ; 2); C(2 ; 0); D(0,5 ; 0)
- P(-3 ; 3) ; Q(-1 ; 1) ; R(-3 ; 1)

a.Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\) (1)
\(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\dfrac{k^2\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\)(2)
Từ (1) và (2) suy ra: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
b.M = \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{50^2}\right)\)
= \(\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}\)
= \(\dfrac{1.3.2.4.3.5...49.51}{2^2.3^2.4^2...50^2}\)
\(\dfrac{51}{2.50}=\dfrac{51}{100}\)
Lời giải:
a)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow \left(\frac{a}{b}\right)^2=\left(\frac{b}{d}\right)^2=\frac{(a+c)^2}{(b+d)^2}(1)\)
Mặt khác, \(\frac{a}{b}=\frac{c}{d}\Rightarrow \frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}(2)\) (áp dụng tính chất dãy tỉ số bằng nhau)
Từ \((1),(2)\Rightarrow \frac{(a+c)^2}{(b+d)^2}=\frac{a^2+c^2}{b^2+d^2}\)
b) Vì \(1-\frac{1}{2^2};1-\frac{1}{3^2};...;1-\frac{1}{50^2}<1\) nên:
\(\left\{\begin{matrix} \left \{ 1-\frac{1}{2^2} \right \}=1-\frac{1}{2^2}\\ \left \{ 1-\frac{1}{3^2} \right \}=1-\frac{1}{3^2}\\ ....\\ \left \{ 1-\frac{1}{50^2} \right \}=1-\frac{1}{50^2}\end{matrix}\right.\)
\(\Rightarrow M=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)....\left(1-\frac{1}{50^2}\right)\)
\(\Leftrightarrow M=\frac{(2^2-1)(3^2-1)(4^2-1)....(50^2-1)}{(2.3....50)^2}\)
\(\Leftrightarrow M=\frac{[(2-1)(3-1)...(50-1)][(2+1)(3+1)...(50+1)]}{(2.3.4...50)^2}\)
\(\Leftrightarrow M=\frac{(2.3...49)(3.4.5...51)}{(2.3.4...50)^2}=\frac{(2.3.4...49)^2.50.51}{2.(2.3....49)^2.50^2}=\frac{50.51}{2.50^2}=\frac{51}{100}\)
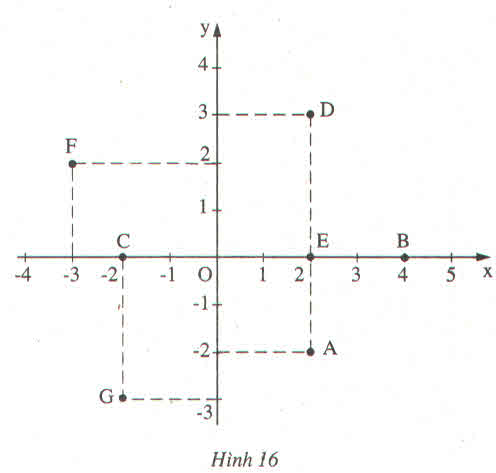




a) Tọa độ các điểm trong hình vẽ là:
A(2;-2); B(4;0); C(-2;0); D(2;3); E(2;0);F(-3;2); G(-2;-3)
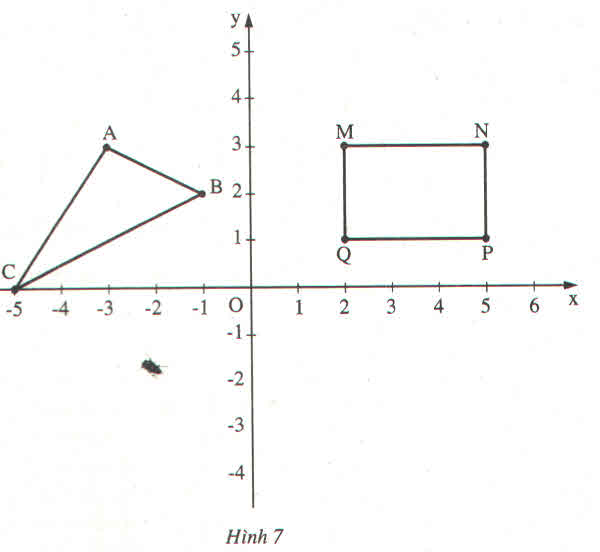
b) Ta có hình vẽ ∆ABC:
A(-3;4); B(-3;1); C(1;-1).