Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A x y B C
b) 2 tia đối gốc A là Ax và Ay
c) ta có Ax và Ay là 2 tia đối nhau
B thuộc ax và c thuộc ay
suy ra a nằm giữa 2 điểm b và c
a)
A x y B C
b) Hai tia đối nhau với gốc A là \(Ax\)và \(Ay\)
c) Ta thấy Ax và Ay là 2 tia đối nhau
và B nằm trên tia Ax; C nằm trên tia Ay
=> A nằm giữa B và C.

Bài này mình ko vẽ hình được, mong bạn thông cảm \(:))\)
a, Trên tia Ox có: \(OA=4cm\) ( đề ) 1
\(OB=7cm\) ( đề ) 2
Từ 1 và 2 \(\Rightarrow\) A nằm giữa O và B ( t/c vẽ hai đoạn thẳng trên tia )
b, Ta có: A nằm giữa O và B ( cmt )
\(\Rightarrow OA+AB=OB\)( t/c cộng độ dài đoạn thẳng )
Thay số: \(4+AB=7\)
\(AB=7-4\)
\(AB=3(cm)\)
Ta có: \(AB=3cm\) ( cmt ) 3
\(OA=4cm\) ( đề ) 4
Từ 3 và 4 \(\Rightarrow AB< OA\)
c, Trên tia BA có: \(BA=3cm\) ( cmt ) 5
\(BC=5cm\) ( đề ) 6
Từ 5 và 6 \(\Rightarrow\) A nằm giữa B và C ( t/c vẽ hai đoạn thẳng trên tia )
\(\Rightarrow BA+CA=BC\) ( t/c cộng độ dài đoạn thẳng )
Thay số: \(3+CA=5\)
\(CA=5-3\)
\(CA=2(cm)\)
Trên tia AO có: \(AC=2cm\) ( cmt ) 7
\(AO=4cm\) ( đề ) 8
Từ 7 và 8 \(\Rightarrow\) \(AC< AO\)
\(\Rightarrow\) C nằm giữa A và O ( t/c vẽ hai đoạn thẳng trên tia )
\(\Rightarrow AC+CO=AO\) ( t/c cộng độ dài đoạn thẳng )
Thay số: \(2+CO=4\)
\(CO=4-2\)
\(CO=2(cm)\)
Ta có: \(CO=2cm\) ( cmt ) 9
\(CA=2cm\) ( cmt ) 10
Từ 9 và 10 \(\Rightarrow CO=CA\)
Mặt khác: C nằm giữa A và O ( cmt )
\(\Rightarrow\) C là trung điểm của OA

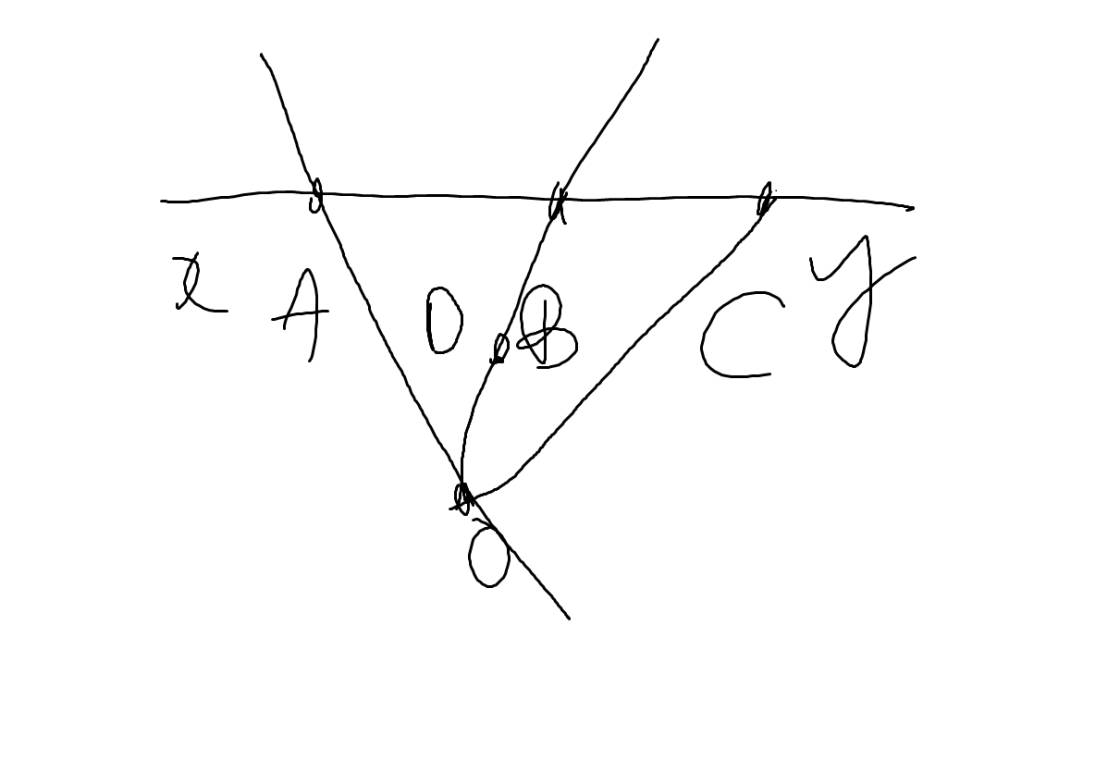
ta có hình vẽ :
y x O A B C D
a, Có 6 tam giác đỉnh O là OAB , OAC , OAD , OBC , OBD , OCD
Ta nhận thấy trên đường thẳng xy có bao nhiêu đoạn thẳng thì khi kết hợp với đỉnh O ta được bấy nhiêu tam giác
b, Nếu trên đường thẳng xy có n điểm A1 , A2 , ..., An thì số đoạn thẳng có trên đường thẳng xy là :
\(\frac{n\left(n-1\right)}{2}\)
Do đó số tam giác đỉnh O có hai đỉnh còn lại là 2 trong n điểm A1 , A2 ,..., An là \(\frac{n\left(n-1\right)}{2}\) ( tam giác ).
TK
a)
b)
:>