K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

3 tháng 4 2017
a) cosx - √3sinx = √2 ⇔ cosx - tan![]() sinx = √2
sinx = √2
⇔ cos![]() cosx - sin
cosx - sin![]() sinx = √2cos
sinx = √2cos![]() ⇔ cos(x +
⇔ cos(x + ![]() ) =
) = ![]()
⇔ 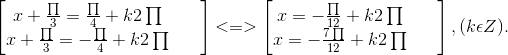
3 tháng 4 2017
b) 3sin3x - 4cos3x = 5 ⇔ ![]() sin3x -
sin3x - ![]() cos3x = 1.
cos3x = 1.
Đặt α = arccos![]() thì phương trình trở thành
thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = ![]() + k2π
+ k2π
⇔ x = ![]() , k ∈ Z (trong đó α = arccos
, k ∈ Z (trong đó α = arccos![]() ).
).
Đkxđ: \(x\in R\).
\(cos2x-cos3x+cos4x=0\Leftrightarrow\left(cos2x+cos4x\right)-cos3x=0\)
\(\Leftrightarrow2cos3x.cosx-cos3x=0\)
\(\Leftrightarrow cos3x\left(2cos2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=0\\2cos2x-1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cos3x=0\\cos2x=\dfrac{1}{2}\end{matrix}\right.\)
\(cos3x=0\Leftrightarrow3x=\dfrac{\pi}{2}+k\pi\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
\(cos2x=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\dfrac{sinB}{sinC}=2cosA\Leftrightarrow sinB=2cosA.sinC\)
\(\Leftrightarrow sinB=sin\left(A+C\right)+sin\left(C-A\right)\)
\(\Leftrightarrow sinB=sin\left(\pi-\left(A+C\right)\right)+sin\left(C-A\right)\)
\(\Leftrightarrow sinB=sinB+sin\left(C-A\right)\)
\(\Leftrightarrow sin\left(C-A\right)=0\) (1)
Do A, C là số đo các góc trong tam giác nên từ (1) suy ra:
\(C=A\) hay tam giác ABC cân.