K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VQ
5
MM
1
15 tháng 1 2018
ĐKXĐ : X khác 1
pt <=> X^2+X+1/(X-1).(X^2+X+1) - 3X^2/(X-1).(X^2+X+1) = 2X.(X-1)/(X-1).(X^2+X+1)
<=> X^2+X+1/(X-1).(X^2+X+1) - 3X^2/(X-1).(X^2+X+1) - 2X^2-2X/(X-1).(X^2+X+1) = 0
<=> X^2+X+1-3X^2-2X^2+2X/(X-1).(X^2+X+1) = 0
<=> X^2+X+1-3X^2-2X^2+2X=0
<=> -4X^2+3X+1=0
<=> 4X^2-3X-1=0
<=> (X-1).(4X+1) = 0
<=> 4X+1=0 ( vì X khác 1 nên X-1 khác 0 )
<=> X = -1/4 (tm)
Vậy pt có tập nghiệm S = {-1/4}
Tk mk nha
24 tháng 11 2018
\(P=1+\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{n\left(n+1\right)}\)
\(=1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{n}-\frac{1}{n+1}\)
\(=2-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{n}-\frac{1}{n+1}\)
\(=2-\frac{1}{n+1}=\frac{2\left(n+1\right)}{n+1}-\frac{1}{n+1}=\frac{2n+2-1}{n+1}=\frac{2n+1}{n+1}\)
YS
3
TT
10 tháng 10 2018
- Bình phương của một tổng:
- Bình phương của một hiệu:
- Hiệu hai bình phương:
- Lập phương của một tổng:
- Lập phương của một hiệu:
- Tổng hai lập phương:
- Hiệu hai lập phương:
Các hệ thức liên quan
NT
1
10 tháng 3 2022
\(a)P=\left(\dfrac{x^2+2}{x^3-1}+\dfrac{x+1}{x^2+x+1}+\dfrac{1}{1-x}\right).\left(\dfrac{x^2}{x+1}+1\right).\left(x\ne1;x\ne-1\right).\\ P=\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}.\dfrac{x^2+x+1}{x+1}.\\ P=\dfrac{x^2-x}{x-1}.\dfrac{1}{x+1}.\\ P=\dfrac{x\left(x-1\right)}{x-1}.\dfrac{1}{x+1}.\\ P=x.\dfrac{1}{x+1}.\\ P=\dfrac{x}{x+1}.\)
\(P=\dfrac{1}{4}.\Rightarrow\dfrac{x}{x+1}=\dfrac{1}{4}.\\ \Leftrightarrow4x-x-1=0.\\ \Leftrightarrow3x-1=0.\\ \Leftrightarrow x=\dfrac{1}{3}\left(TM\right).\)
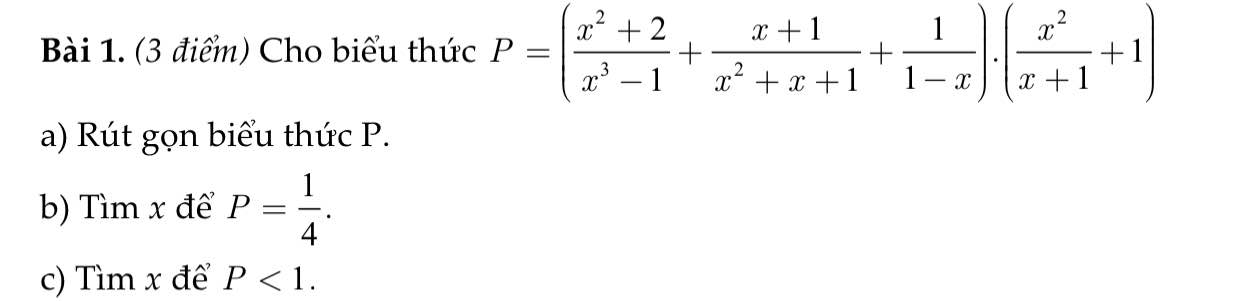
bằng 2 chả lẽ lại đố mẹo
= 2
Hello bạn
Mình kết bạn rồi nhé