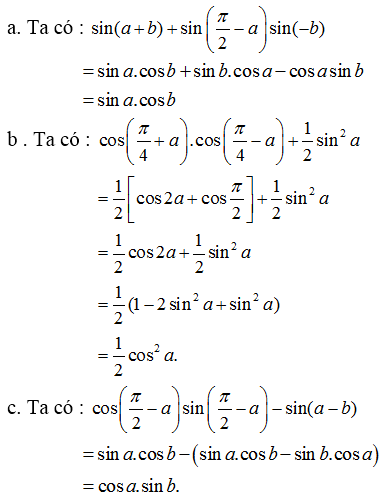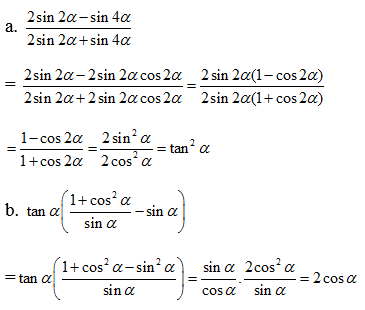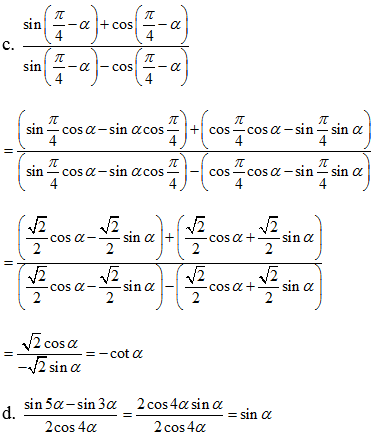Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A=sin\left(\dfrac{\pi}{4}+x\right)-cos\left(\dfrac{\pi}{4}-x\right)\)
\(\Leftrightarrow A=sin\dfrac{\pi}{4}.cosx+cos\dfrac{\pi}{4}.sinx-\left(cos\dfrac{\pi}{4}.cosx+sin\dfrac{\pi}{4}.sinx\right)\)
\(\Leftrightarrow A=sin\dfrac{\pi}{4}.cosx+cos\dfrac{\pi}{4}.sinx-cos\dfrac{\pi}{4}.cosx-sin\dfrac{\pi}{4}.sinx\)
\(\Leftrightarrow A=\dfrac{\sqrt{2}}{2}.cosx+\dfrac{\sqrt{2}}{2}.sinx-\dfrac{\sqrt{2}}{2}.cosx-\dfrac{\sqrt{2}}{2}.sinx\)
\(\Leftrightarrow A=0\)
b) \(B=cos\left(\dfrac{\pi}{6}-x\right)-sin\left(\dfrac{\pi}{3}+x\right)\)
\(\Leftrightarrow B=cos\dfrac{\pi}{6}.cosx+sin\dfrac{\pi}{6}.sinx-\left(sin\dfrac{\pi}{3}.cosx+cos\dfrac{\pi}{3}.sinx\right)\)
\(\Leftrightarrow B=cos\dfrac{\pi}{6}.cosx+sin\dfrac{\pi}{6}.sinx-sin\dfrac{\pi}{3}.cosx-cos\dfrac{\pi}{3}.sinx\)
\(\Leftrightarrow B=\dfrac{\sqrt{3}}{2}.cosx+\dfrac{1}{2}.sinx-\dfrac{\sqrt{3}}{2}.cosx-\dfrac{1}{2}.sinx\)
\(\Leftrightarrow B=0\)
c) \(C=sin^2x+cos\left(\dfrac{\pi}{3}-x\right).cos\left(\dfrac{\pi}{3}+x\right)\)
\(\Leftrightarrow C=sin^2x+\left(cos\dfrac{\pi}{3}.cosx+sin\dfrac{\pi}{3}.sinx\right).\left(cos\dfrac{\pi}{3}.cosx-sin\dfrac{\pi}{3}.sinx\right)\)
\(\Leftrightarrow C=sin^2x+\left(\dfrac{1}{2}.cosx+\dfrac{\sqrt{3}}{2}.sinx\right).\left(\dfrac{1}{2}.cosx-\dfrac{\sqrt{3}}{2}.sinx\right)\)
\(\Leftrightarrow C=sin^2x+\dfrac{1}{4}.cos^2x-\dfrac{3}{4}.sin^2x\)
\(\Leftrightarrow C=\dfrac{1}{4}.sin^2x+\dfrac{1}{4}.cos^2x\)
\(\Leftrightarrow C=\dfrac{1}{4}\left(sin^2x+cos^2x\right)\)
\(\Leftrightarrow C=\dfrac{1}{4}\)
d) \(D=\dfrac{1-cos2x+sin2x}{1+cos2x+sin2x}.cotx\)
\(\Leftrightarrow D=\dfrac{1-\left(1-2sin^2x\right)+2sinx.cosx}{1+2cos^2a-1+2sinx.cosx}.cotx\)
\(\Leftrightarrow D=\dfrac{2sin^2x+2sinx.cosx}{2cos^2x+2sinx.cosx}.cotx\)
\(\Leftrightarrow D=\dfrac{2sinx\left(sinx+cosx\right)}{2cosx\left(cosx+sinx\right)}.cotx\)
\(\Leftrightarrow D=\dfrac{sinx}{cosx}.cotx\)
\(\Leftrightarrow D=tanx.cotx\)
\(\Leftrightarrow D=1\)

rút gọn biểu thức:
E=cos(\(\dfrac{3\pi}{3}-\alpha\))-sin(\(\dfrac{3\pi}{2}-\alpha\))+sin(\(\alpha+4\pi\))

a) \(a=12,4\pi=12\pi+0,4\pi=6.2\pi+0,4\pi\).
Suy ra: \(x=0,4\pi\).
b) \(a=-\dfrac{9}{5}\pi=-2\pi+\dfrac{1}{5}\pi\).
Suy ra: \(x=\dfrac{1}{5}\pi\).
c) \(a=\dfrac{13}{4}\pi=2\pi+\dfrac{5}{4}\pi\)
Suy ra: \(x=\dfrac{5}{4}\pi\).

\(A=\dfrac{4sin^4x-cos^2x\left(1-cos^2x\right)+sin^2x.cos^2x-2cos^2x}{sin^2x}+\dfrac{2}{tan^2x}\)
\(=\dfrac{4sin^4x-sin^2x.cos^2x+sin^2x.cos^2x-2cos^2x}{sin^2x}+2cot^2x\)
\(=4sin^2x-2cot^2x+2cot^2x=4sin^2x\)
\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=2\end{matrix}\right.\)

Phương trình tương đương với :
\(\left\{{}\begin{matrix}\dfrac{\pi}{2}\cos\left(x-\dfrac{\pi}{4}\right)=\dfrac{\pi}{4}+2k\pi\\\dfrac{\pi}{2}\cos\left(x-\dfrac{\pi}{4}\right)=-\dfrac{\pi}{4}+2k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\cos\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}+4k\left(1\right)\\\cos\left(x-\dfrac{\pi}{4}\right)=-\dfrac{1}{2}+4k\left(2\right)\end{matrix}\right.k\in Z\)
Phương trình (1) có nghiệm khi và chỉ khi :
\(\left|\dfrac{1}{2}+4k\right|\le1\Leftrightarrow\dfrac{-3}{8}\le k\le\dfrac{1}{8}\Leftrightarrow k=0\left(k\in Z\right)\)
Khi đó (1) có dạng :
\(\cos\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{3}+2l\pi\\x-\dfrac{\pi}{4}=-\dfrac{\pi}{3}+2l\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7\pi}{12}+2l\pi\\x=\dfrac{-\pi}{12}+2l\pi\end{matrix}\right.l\in Z\left(3\right)\)
Phương trình (2) có nghiệm khi và chỉ khi :
\(\left|-\dfrac{1}{2}+4k\right|\le1\Leftrightarrow\dfrac{-1}{8}\le k\le0\left(k\in Z\right)\)
Khi đó (2) có dạng :
\(\cos\left(x-\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{2\pi}{3}+2l\pi\\x-\dfrac{\pi}{4}=-\dfrac{2\pi}{3}+2l\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11\pi}{12}+2l\pi\\x=\dfrac{-5\pi}{12}+2l\pi\end{matrix}\right.l\in Z\left(4\right)\)
Kết hợp (3),(4) ta có :
\(\left\{{}\begin{matrix}x=\dfrac{11\pi}{12}+l\pi\\x=\dfrac{7\pi}{12}+l\pi\end{matrix}\right.,l\in Z\)
Vậy phương trình có 2 bộ nghiệm