Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: p = 42k + r= (2×3×7)k +r( k,r thuộc N, r lớn hơn 0 và bé hơn 42). Vì p là số nguyên tố nên r ko chia hết cho 2,3,7.
Các hợp số nhỏ hơn 42 và ko chia hết cho2 là 9,15,21,25,27,33,35,39.
Loại bỏ các số chia hết cho 3, cho 7, chỉ còn 25
Vậy r là 25

Vì r là hợp số nên r và 42 là nguyên tố cùng nhau
Vì 42 = 2 x 3 x 7 nên R không chia hết cho 2, 3 và 7 hoặc bội của chúng
Trong các số từ 1 đến 41 chỉ có 5 và 25 thỏa mãn
Vì r là hợp số nên chọn r = 25 thỏa mãn đầu bài
Ta có :
p = 42k + r = 2 . 3 . 7 k + r ( k , r \(\in\)N , 0 < r < 42 ) . Vì p là số nguyên tố nên r không chia hết cho 2 , 3 , 7 .
Các hợp số nhỏ hơn 42 và không chia hết cho 2 là 9 , 15 , 21 , 25 , 27 , 33 , 35 , 39 .
Loại đi các số chia hết cho 3 , 7 , chỉ còn 25 .
Vậy r = 25


ta có : nếu P=3 suy ra :8P+1=25 chia hết cho 5
8P-1=23(số nguyên tố)
Vậy P=3 thỏa mãn yêu cầu của đề bải
nếu P >3 =>P;P+1:P-1 sẽ phải có 1 số chia hết cho 3 mà P là số nguyên tố lớn hơn 3=>P-1 hoắc P+1 chia hết cho 3=>(P-1)(P+1) chia hết cho 3
=>(8P-1)(8P+1) chia hết cho 3
=64p^2-1=63P^2+P^2-1=3.21P^2 chia hết cho 3
vậy 8p+1 là hớp số(chia hết cho 3)

Ta có
(●>ω<● ) •✫ ✾♕ TiỂu NgƯ nHI (☆▽☆)(ღ˘⌣˘ღ) (⊂(♡⌂♡)⊃
bạn copy nên mới không thể đổi phông chữ được chứ gì

Trl :
Ta có :
\(P=42.k+r.=2.3.7.k+r\)
Vì \(r\)là hợp số và \(r< 42\)nên \(r\)phải là tích của 2 số \(r\)\(=x.y\)
\(x,y\)không thể là \(2,3,7\)và cũng không thể là số \(⋮2,3,7\)được vì thế thì \(P\)không là số nguyên tố
Vậy \(x,y\)có thể là \(\left\{5,11,13,...\right\}\)
Nếu \(x=5\)và \(y=11\)thì\(r=x.y\)= \(55>43\)
Vậy chỉ còn trường hợp : \(x=5\), \(y=5\). Khi đó , \(r=25\)

Ta có:
p = 42.k + r. = 2.3.7.k + r
Vì r là hợp số và r < 42 nên r phải là tích của 2 số r = x.y
x và y không thể là 2, 3, 7 và cũng không thể là số chia hết cho 2, 3, 7 được vì nếu thế thì p không là số nguyên tố.
Vậy x và y có thể là các số trong các số {5,11,13, ..}
Nếu x=5 và y=11 thì r = x.y =55>42
Vậy chỉ còn trường hợp x = 5, y = 5. Khi đó r = 25.
ta có
p= 42.k +r= 2.3.7.k+r
vì r là hợp số r <42 r hpair phân tích 2 số r = x.y
x,y không thể là 2,3,7 và cũng không thể là số chia hết cho được vì thế p là số nguyên tố
vậy x,y [ 5,11, 13]
nếu x=5 và y = 11 thì r.y = 55 >43
vậy chỉ còn trường hợp x=5 r = 5. khi đó r = 25


Ta có :\(p = 42k + r = 2.3.7.k + r( k , r thuộc N , 0< r <42)\)
Vì p là số nguyên tố nên r không chia hết cho 2, 3, 7.
Các hợp số nhỏ hơn 42 và không chia hết cho 2 là 9, 15, 21, 25, 27, 33, 35, 39.
Loại đi các số chia hết cho 3, cho 7, chỉ còn 25.
Vậy r = 25.
Kết luận. Nếu p và 8p-1 là số nguyên tố thì 8p+1 là hợp số.
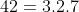 .
.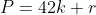 .
.
2. Một số nguyên tố P chia cho 42 có số dư r là hợp số .Tìm r ?
Lời giải. Phân tích
Ta có
Xét
Ta có: p= 42 a + r = 2.3.7 a + r (a,b thuộc N; 0< r <42)
* Vì p là số nguyên tố nên r không chia hết cho 2;3;7.
Các hợp số nhỏ hơn 42 không chia hết cho 2 là {9;15;21;25;27;33;35;39}
Loại bỏ các số chia hết cho 3, cho 7 ta còn có số 25
=> Vậy r = 25