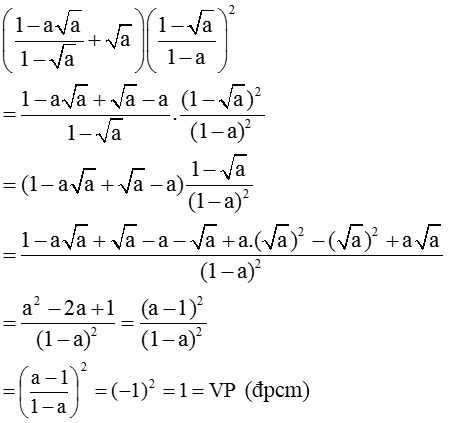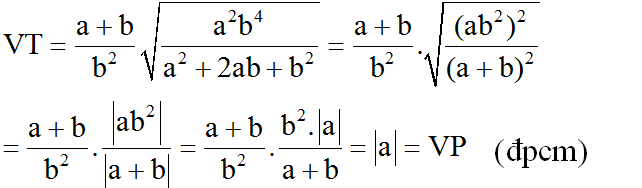Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mấy bài cơ bản nên cũng dễ, mk có thể giải hết cho bn vs 1 đk : bn đăng từng câu 1 thôi nhé !
bài 3 có thể lên gg tìm kỹ thuật AM-GM (cosi) ngược dấu
bài 8 c/m bđt phụ 5b3-a3/ab+3b2 </ 2b-a ( biến đổi tương đương)
những câu còn lại 1 nửa dùng bđt AM-GM , 1 nửa phân tích nhân tử ròi dựa vào điều kiện

Ta cm bằng cách bđ tương đương
\(Cm:ab\left(a+b\right)^2\le\frac{1}{64}\Leftrightarrow64ab\left(a+b\right)^2\le1\Leftrightarrow8\left(a+b\right)\sqrt{ab}\le1.\)
Ta có:
\(8\left(a+b\right)\sqrt{ab}=4.\left(a+b\right).2\sqrt{ab}\le4.\frac{a+b+2\sqrt{ab}}{4}=\left(\sqrt{a}+\sqrt{b}\right)^2=1\left(đpcm\right)\)
Dấu "=" xảy ra khi \(a=b=\frac{1}{4}\)

\(VT\le\sqrt{\left(1+1\right)\left(2ab+a+b\right)}\)
\(\le\sqrt{\left(1+1\right)\left(\frac{\left(a+b\right)^2}{2}+a+b\right)}\)
\(\le\sqrt{\left(1+1\right)\left(\frac{2^2}{2}+2\right)}=2\sqrt{2}\)
Dấu "=" khi \(a=b=1\)

Từ kết quả bài toán suy ngược ra thôi
Muốn giải thích thì cứ phá 2 vế ra rồi so sánh là tìm ra cách tách biểu thức
Câu 4 mình ko biết giải quyết kiểu lớp 9 (mặc dù chắc chắn là biểu thức sẽ được biến đổi như vầy)
Đó là kiểu trình bày của lớp 11 hoặc 12 để bạn tham khảo thôi

2, a, \(a+\dfrac{1}{a}\ge2\)
\(\Leftrightarrow\dfrac{a^2+1}{a}\ge2\)
\(\Rightarrow a^2-2a+1\ge0\left(a>0\right)\)
\(\Leftrightarrow\left(a-1\right)^2\ge0\)( là đt đúng vs mọi a)
vậy...................
Câu 1:
\(M=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{\left(2+\sqrt{3}\right)^2}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-20-10\sqrt{3}}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{\left(5-\sqrt{3}\right)^2}}}\)
\(=\sqrt{4+\sqrt{5\sqrt{3}+25-5\sqrt{3}}}\)
\(=\sqrt{4+5}=3\)
\(M=\sqrt{5-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)
\(=\sqrt{5-\sqrt{3-\sqrt{\left(2\sqrt{5}-3\right)^2}}}\)
\(=\sqrt{5-\sqrt{3-2\sqrt{5}+3}}\)
\(=\sqrt{5-\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(=\sqrt{5-\sqrt{5}+1}=\sqrt{6-\sqrt{5}}\)

Ta có \(\sqrt{3b\left(a+2b\right)}\le\frac{1}{2}\left(3b+a+2b\right)=\frac{1}{2}\left(a+5b\right)\)
\(\sqrt{3a\left(b+2a\right)}\le\frac{1}{2}\left(5a+b\right)\)
=> \(P\le\frac{1}{2}\left(a^2+b^2+10ab\right)\)
Mà \(ab\le\frac{1}{2}\left(a^2+b^2\right)\le\frac{1}{2}.2=1\)
=> \(P\le\frac{1}{2}\left(2+10\right)=6\)
Vậy MaxP=6 khi a=b=1