Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
(1)\(cos\left(x\right)-sin\left(x\right)=\sqrt{2}.\dfrac{\sqrt{2}}{2}\left(cos\left(x\right)-sin\left(x\right)\right)\\ =\sqrt{2}.\left(\dfrac{\sqrt{2}}{2}.cos\left(x\right)-\dfrac{\sqrt{2}}{2}.sin\left(x\right)\right)\\ =\sqrt{2}.\left(sin\dfrac{\pi}{4}cos\left(x\right)-cos\dfrac{\pi}{4}.sin\left(x\right)\right)\\ =\sqrt{2}.sin\left(\dfrac{\pi}{4}-x\right)\)
(2) \(cos\left(x\right)+sin\left(x\right)=\sqrt{2}.\dfrac{\sqrt{2}}{2}\left(cos\left(x\right)+sin\left(x\right)\right)\\ =\sqrt{2}.\left(\dfrac{\sqrt{2}}{2}.cos\left(x\right)+\dfrac{\sqrt{2}}{2}.sin\left(x\right)\right)\\ =\sqrt{2}.\left(cos\dfrac{\pi}{4}cos\left(x\right)+sin\dfrac{\pi}{4}.sin\left(x\right)\right)\\ =\sqrt{2}.cos\left(x-\dfrac{\pi}{4}\right)\)
ADCT trên ta được:
\(sin\left(x\right)+\sqrt{2}.sin\left(\dfrac{\pi}{2}-x\right)=\sqrt{2}\\ \Leftrightarrow sin\left(x\right)+\sqrt{2}.sin\left(\dfrac{\pi}{4}-\left(x-\dfrac{\pi}{4}\right)\right)=\sqrt{2}\\ \Leftrightarrow sin\left(x\right)+cos\left(x-\dfrac{\pi}{4}\right)-sin\left(x-\dfrac{\pi}{4}\right)=\sqrt{2}\\ \sqrt{2}sin\left(x\right)+\sqrt{2}cos\left(x-\dfrac{\pi}{4}\right)+\sqrt{2}sin\left(\dfrac{\pi}{4}-x\right)=2\\ \Leftrightarrow\sqrt{2}sin\left(x\right)+cos\left(x\right)+sin\left(x\right)+cos\left(x\right)-sin\left(x\right)=2\\ \Leftrightarrow\sqrt{2}sin\left(x\right)+2cos\left(x\right)=2\)
Đến đây lại dùng cách trong sgk giải pt: a.sin(x) + b.cos(x) = c tìm ra x để thay nhá

a: pi/2<x<pi
=>cosx<0
=>\(cosx=-\sqrt{1-\left(\dfrac{1}{5}\right)^2}=-\dfrac{2\sqrt{6}}{5}\)
\(sin2x=2\cdot sinx\cdot cosx=2\cdot\dfrac{1}{5}\cdot\dfrac{-2\sqrt{6}}{5}=\dfrac{-4\sqrt{6}}{25}\)
\(cos2x=2\cdot cos^2x-1=2\cdot\dfrac{24}{25}-1=\dfrac{48}{25}-1=\dfrac{23}{25}\)
\(tan2x=-\dfrac{4\sqrt{6}}{25}:\dfrac{23}{25}=-\dfrac{4\sqrt{6}}{23}\)
\(cot2x=1:\dfrac{-4\sqrt{6}}{23}=\dfrac{-23}{4\sqrt{6}}\)
b: \(sin\left(x-\dfrac{pi}{6}\right)=sinx\cdot cos\left(\dfrac{pi}{6}\right)-cosx\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=sinx\cdot\dfrac{\sqrt{3}}{2}-cosx\cdot\dfrac{1}{2}\)
\(=\dfrac{1}{5}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{-2\sqrt{6}}{5}\cdot\dfrac{1}{2}=\dfrac{\sqrt{3}+2\sqrt{6}}{10}\)
c: \(cos\left(x-\dfrac{pi}{3}\right)=cosx\cdot cos\left(\dfrac{pi}{3}\right)+sinx\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=-\dfrac{2\sqrt{6}}{5}\cdot\dfrac{1}{2}+\dfrac{1}{5}\cdot\dfrac{1}{2}=\dfrac{-2\sqrt{6}+1}{10}\)
d: \(tan\left(x-\dfrac{pi}{4}\right)=\dfrac{tanx-tan\left(\dfrac{pi}{4}\right)}{1+tanx\cdot tan\left(\dfrac{pi}{4}\right)}\)
\(=\dfrac{tanx-1}{1+tanx}\)
\(=\dfrac{\dfrac{1}{-2\sqrt{6}}-1}{1+\dfrac{1}{-2\sqrt{6}}}=\dfrac{-25-4\sqrt{6}}{23}\)

a: pi<x<3/2pi
=>cosx<0
=>\(cosx=-\sqrt{1-\left(-\dfrac{3}{5}\right)^2}=-\dfrac{4}{5}\)
\(tanx=\dfrac{-3}{5}:\dfrac{-4}{5}=\dfrac{3}{4}\)
cot x=1:3/4=4/3
\(sin2x=2\cdot sinx\cdot cosx=2\cdot\dfrac{-3}{5}\cdot\dfrac{-4}{5}=\dfrac{24}{25}\)
\(cos2x=1-2\cdot sin^2x=1-2\cdot\left(-\dfrac{3}{5}\right)^2=\dfrac{7}{25}\)
\(tan2x=\dfrac{24}{25}:\dfrac{7}{25}=\dfrac{24}{7}\)
cot 2x=1:24/7=7/24
b: \(sin\left(x+\dfrac{pi}{3}\right)=sinx\cdot cos\left(\dfrac{pi}{3}\right)+sin\left(\dfrac{pi}{3}\right)\cdot cosx\)
\(=\dfrac{-3}{5}\cdot\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\cdot\dfrac{-4}{5}=\dfrac{-3-4\sqrt{3}}{10}\)

1/ ĐKXĐ: \(sinx\ne0\)
\(\Leftrightarrow a.cos2x+sinx=\frac{cos^2x}{sinx}\)
\(\Leftrightarrow a.cos2x.sinx+sin^2x-cos^2x=0\)
\(\Leftrightarrow a.cos2x.sinx-cos2x=0\)
\(\Leftrightarrow cos2x\left(a.sinx-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cos2x=0\Rightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\\a.sinx-1=0\left(1\right)\end{matrix}\right.\)
Do \(cos2x=0\) có 4 nghiệm trên khoảng đã cho nên để pt có đúng 4 nghiệm thì (1) vô nghiệm hoặc có nghiệm \(sinx=0\)
Với \(a=0\Rightarrow-1=0\) pt vô nghiệm (thỏa mãn)
Với \(a\ne0\Rightarrow sinx=\frac{1}{a}\Rightarrow\) để pt vô nghiệm thì \(\left|\frac{1}{a}\right|>1\Rightarrow-1< a< 1\)
Vậy \(-1< a< 1\)
2/
\(\Leftrightarrow4cos^3x-3cosx-\left(2cos^2x-1\right)+m.cosx-1=0\)
\(\Leftrightarrow4cos^3x-3cosx-2cos^2x+m.cosx=0\)
\(\Leftrightarrow cosx\left(4cos^2x-2cosx+m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\4cos^2x-2cosx+m-3=0\left(1\right)\end{matrix}\right.\)
Do \(cosx=0\) có 2 nghiệm thuộc \(\left(-\frac{\pi}{2};2\pi\right)\) , dựa vào đường tròn lượng giác ta thấy để pt có 7 nghiệm khác nhau thuộc khoảng đó thì (1) có 5 nghiệm sao cho \(-1< cosx_1< 0< cosx_2< 1\)
Đặt \(cosx=a\Rightarrow4a^2-2a+m-3=0\) (2)
Ta cần tìm m để (2) có 2 nghiệm thỏa mãn \(-1< a_1< 0< a_2< 1\)
Để (2) có 2 nghiệm trái dấu thì \(4\left(m-3\right)< 0\Rightarrow m< 3\)
Để (2) có 2 nghiệm thỏa mãn \(-1< a_1< a_2< 1\) thì:
\(\left\{{}\begin{matrix}f\left(-1\right)>0\\f\left(1\right)>0\\-1< \frac{S}{2}< 1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m>-3\\m>1\\-1< \frac{1}{4}< 1\end{matrix}\right.\) \(\Rightarrow m>1\)
Vậy \(1< m< 3\)

1. \(pt\Leftrightarrow \tan 2x(1-\cos 2x)-(1-\cos 2x)=0\Leftrightarrow (\tan 2x-1)(1-\cos 2x)=0\)
2. Đặt \(t=\sin x+\cos x\Rightarrow t^2=1+2\sin x.\cos x\) thay vào phương trình ta được
\(t-3(t^2-1)=1\Leftrightarrow 3t^2-t-2=0\)
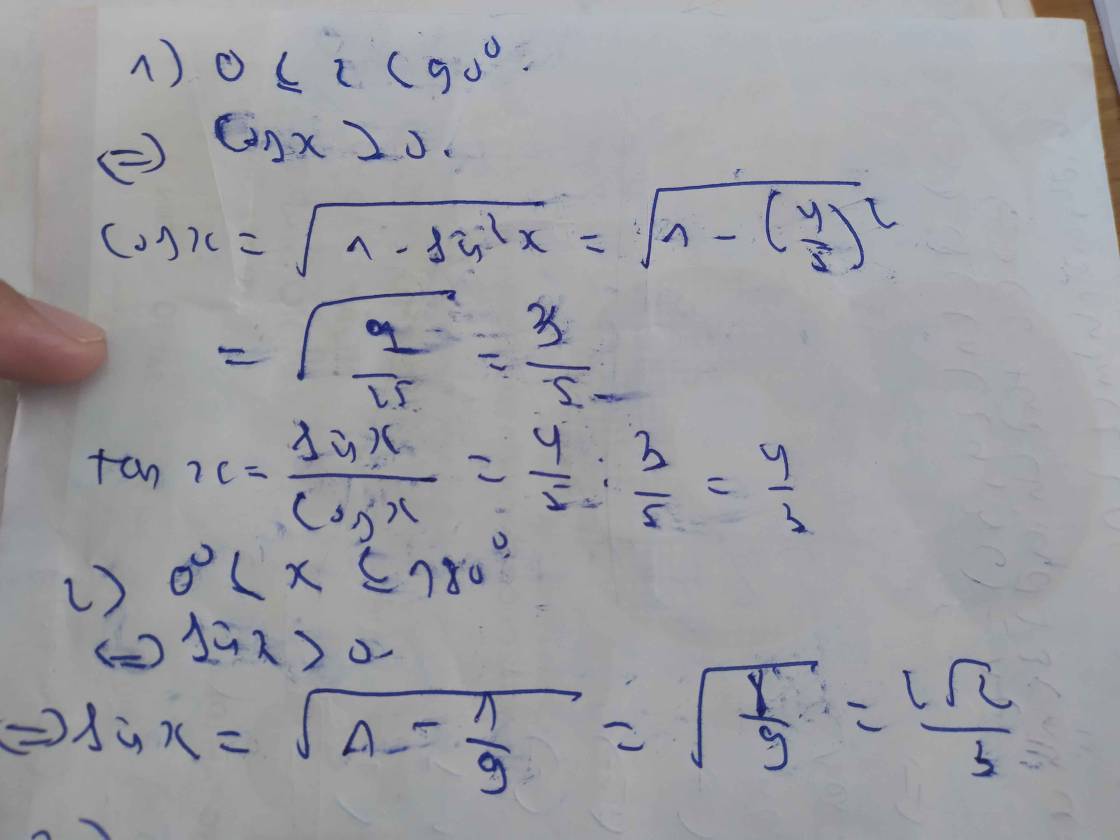

1: 90<x<180
=>cosx<0
=>\(cosx=-\sqrt{1-\left(\dfrac{4}{5}\right)^2}=-\dfrac{3}{5}\)
\(sin2x=2\cdot sinx\cdot cosx=2\cdot\dfrac{4}{5}\cdot\dfrac{-3}{5}=\dfrac{-24}{25}\)
\(cos2x=2\cdot cos^2x-1=2\cdot\dfrac{9}{25}-1=-\dfrac{7}{25}\)
\(tan2x=\dfrac{-24}{25}:\dfrac{-7}{25}=\dfrac{24}{7}\)
2: 0<x<90
=>cosx>0
=>\(cosx=\sqrt{1-\left(\dfrac{1}{2}\right)^2}=\dfrac{\sqrt{3}}{2}\)
\(cos2x=2\cdot cos^2x-1=2\cdot\dfrac{3}{4}-1=\dfrac{6}{4}-1=\dfrac{2}{4}=\dfrac{1}{2}\)