Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp:
+) Gọi M(x;y;z) tọa độ các véc tơ A M → , B M →
+) Gọi H, K lần lượt là hình chiếu của A,B lên ( α ) , có AMH = BMK
+) Tính sin các góc AMH = BMK và suy ra đẳng thức. Tìm quỹ tích điểm M là một đường tròn.
+) Tính tâm của đường tròn quỹ tích đó.
Cách giải:
Gọi M(x;y;z)
![]()
![]()
Gọi H, K lần lượt là hình chiếu của A, B lên ( α ) có AMH = BMK
![]()
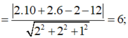
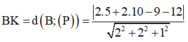
= 3
Khi đó

![]()
Suy ra
![]()
![]()
![]()

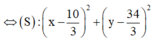
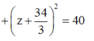

Vậy M ∈ (C) là giao tuyến của ( α ) và (S). Tâm K của (C) là hình chiếu của
I 10 3 ; 34 3 ; - 34 3 trên mặt phẳng ( α ) .
Phương trình đương thẳng đi qua I và vuông góc với ( α ) có dạng
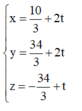
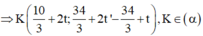
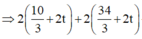
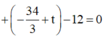
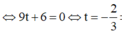
![]()

Chọn B
Gọi A (0;0;a). Đường thẳng AB qua A và vuông góc với (α) có phương trình 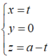
B là hình chiếu của A lên (α) nên tọa độ B thỏa mãn hệ
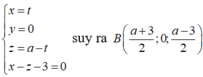
Tam giác MAB cân tại M nên
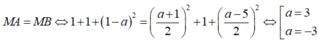
·Nếu a=-3 thì tọa độ A (0;0;-3) và B (0;0;-3) trùng nhau, loại.
·Nếu a=3 thì tọa độ A (0;0;3), B (3;0;0).
Diện tích tam giác MAB bằng 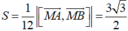

Chọn C

Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
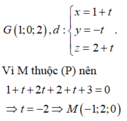

Đáp án C
Phương pháp:
+) Gọi A(0;0;a) (a>0) viết phương trình đường thẳng AB đi qua A và vuông góc với ( α )
![]()
tìm tọa độ điểm B theo a
+) Tam giác MAB cân tại M => MA = MB, tìm a.
+) Sử dụng công thức tính diện tích
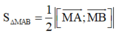
Cách giải:
![]()
=> Phương trình đường thẳng
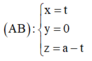
![]()
![]()
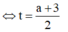
Khi đó
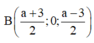
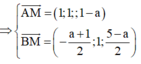
![]()
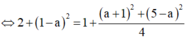
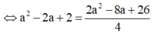
![]()
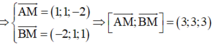
Vậy diện tích tam giác MAB là
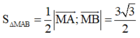

Xét phương trình:
2(1 + 2t) + (t) + (−2 – 3t) – 1 = 0 ⇔ 2t – 1= 0 ⇔ t = 1/2
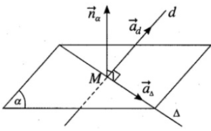
Vậy đường thẳng d cắt mặt phẳng ( α ) tại điểm M(2; 1/2; −7/2).
Ta có vecto pháp tuyến của mặt phẳng ( α ) và vecto chỉ phương của đường thẳng d lần lượt là n α → = (2; 1; 1) và a d → = (2; 1; −3).
Gọi a ∆ → là vecto pháp tuyến của Δ, ta có a ∆ → ⊥ n α → và a ∆ → ⊥ a d →
Suy ra a ∆ → = n α → ∧ n d → = (−4; 8; 0) hay a ∆ → = (1; −2; 0)
Vậy phương trình tham số của
∆
là 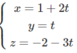

Chọn B
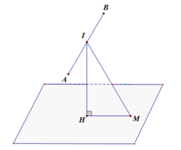
Gọi I là trung điểm AB => I(3;1;4). Gọi H là hình chiếu của I xuống mặt phẳng α .
Ta có
![]()
![]()
Do IA không đổi nên M A → . M B → nhỏ nhất khi MI nhỏ nhất .
![]()
Gọi ∆ là đường thẳng đi qua I và vuông góc với mặt phẳng α . Khi đó ∆ nhận
![]()
Do đó ∆ có phương trình
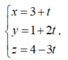
![]()
![]()
![]()
![]()
![]()
Thay tọa độ A và B vào pt \(\left(\alpha\right)\) ra 2 kết quả cùng dấu, do đó A và B nằm cùng phía so với \(\left(\alpha\right)\)
Gọi (d) là đường qua A và vuông góc \(\left(\alpha\right)\), phương trình (d) có dạng:
\(\left\{{}\begin{matrix}x=1+2t\\y=1+t\\z=1-t\end{matrix}\right.\)
Gọi C là giao điểm (d) và \(\left(\alpha\right)\Rightarrow\) tọa độ C tỏa mãn:
\(2\left(1+2t\right)+1+t-\left(1-t\right)+3=0\Rightarrow t=-\dfrac{5}{6}\) \(\Rightarrow C\left(-\dfrac{2}{3};-\dfrac{1}{6};\dfrac{11}{6}\right)\)
Gọi D là điểm đối xứng A qua \(\left(\alpha\right)\Rightarrow\) C là trung điểm AD \(\Rightarrow D\left(-\dfrac{7}{3};-\dfrac{4}{3};\dfrac{8}{3}\right)\)
Do D đối xứng A qua \(\left(\alpha\right)\Rightarrow MA=MD\Rightarrow MA+MB=MD+MB\ge BD\)
Dấu = xảy ra khi B, D, M thẳng hàng hay M là giao của BD và \(\left(\alpha\right)\)
\(\overrightarrow{DB}=\left(\dfrac{13}{3};\dfrac{4}{3};-\dfrac{11}{3}\right)\Rightarrow\)BD nhận (13;4;-11) là 1 vtcp
Phương trình BD: \(\left\{{}\begin{matrix}x=2+13t\\y=4t\\z=-1-11t\end{matrix}\right.\)
\(\Rightarrow\) Tọa độ M thỏa mãn:
\(2\left(2+13t\right)+4t-\left(-1-11t\right)+3=0\Rightarrow t=-\dfrac{8}{41}\)
\(\Rightarrow M\left(-\dfrac{22}{41};-\dfrac{32}{41};\dfrac{47}{41}\right)\)