Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài sai, ví dụ: với \(a=b=1\) thì \(x^2+x-1=0\) có 1 nghiệm thuộc \(\left(0;1\right)\) thỏa mãn yêu cầu
Nhưng \(x^2-2x+1=0\) có nghiệm kép, không phải hai nghiệm phân biệt

a) Hàm số f(x) = 2x3 + 6x + 1 là hàm đa thức nên liên tục trên R.
Mặt khác vì f(0).f(1) = 1.(-3) < 0 nên phương trình có nghiệm trong khoảng (1; 2).
Vậy phương trình f(x) = 0 có ít nhất hai nghiệm.
b) Hàm số g(x) = cosx - x xác định trên R nên liên tục trên R.
Mặt khác, ta có g(0).g() = 1. (-
) < 0 nên phương trình đã cho có nghiệm trong khoảng (0;
).

- Đặt f(x) = (x – a).(x - b) + (x - b).(x - c)+ (x – c).(x- a) thì f(x) liên tục trên R.
- Không giảm tính tổng quát, giả sử a ≤ b ≤ c
- Nếu a = b hoặc b = c thì f(b) = ( b - a).(b - c) = 0 suy ra phương trình có nghiệm x = b.
- Nếu a < b < c thì f(b) = (b - a)(b - c) < 0 và f(a) = (a - b).(a - c) >) 0
do đó tồn tại x 0 thuộc khoảng (a, b) để f x 0 = 0
- Vậy phương trình đã cho luôn có ít nhất một nghiệm.

a) Hàm số f(x) = 2x3 + 6x + 1 là hàm đa thức nên liên tục trên R.
Mặt khác vì f(0).f(1) = 1.(-3) < 0 nên phương trình có nghiệm trong khoảng (1; 2).
Vậy phương trình f(x) = 0 có ít nhất hai nghiệm.
b) Hàm số g(x) = cosx – x xác định trên R nên liên tục trên R.
Mặt khác, ta có g(0).g(π/2) = 1. (-π/2) < 0 nên phương trình đã cho có nghiệm trong khoảng (0; π/2).
a) Hàm số f(x) = 2x3 + 6x + 1 là hàm đa thức nên liên tục trên R.
Mặt khác vì f(0).f(1) = 1.(-3) < 0 nên phương trình có nghiệm trong khoảng (1; 2).
Vậy phương trình f(x) = 0 có ít nhất hai nghiệm.
b) Hàm số g(x) = cosx - x xác định trên R nên liên tục trên R.
Mặt khác, ta có g(0).g() = 1. (-
) < 0 nên phương trình đã cho có nghiệm trong khoảng (0;
).

Chứng minh rằng phương trình sau có ít nhất hai nghiệm :
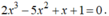
- Xét hàm số: f ( x ) = 2 x 3 - 5 x 2 + x + 1 là hàm đa thức.
⇒ Hàm số f liên tục trên R.
- Ta có:
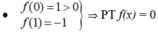 có ít nhất một nghiệm c1 ∈ (0;1).
có ít nhất một nghiệm c1 ∈ (0;1).
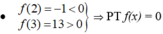 có ít nhất một nghiệm c2 ∈ (2;3).
có ít nhất một nghiệm c2 ∈ (2;3).
- Mà c ≠ c 2 nên PT f(x) = 0 có ít nhất 2 nghiệm.

Ta có:
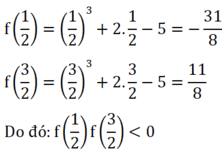
y = f(x) là hàm số đa thức liên tục trên R.
Do đó f(x)liên tục trên 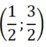
Từ đó suy ra, phương trình f(x) = 0 có ít nhất một nghiệm xo ∈ (0;2)

Đặt f(x) = 2x3 – 6x + 1
TXĐ: D = R
f(x) là hàm đa thức nên liên tục trên R.
Ta có: f(-2) = 2.(-2)3 – 6(-2) + 1 = - 3 < 0
f(0) = 1 > 0
f(1) = 2.13 – 6.1 + 1 = -3 < 0.
⇒ f(-2).f(0) < 0 và f(0).f(1) < 0
⇒ f(x) = 0 có ít nhất một nghiệm thuộc khoảng (-2; 0) và ít nhất một nghiệm thuộc (0 ; 1)
⇒ phương trình f(x) = 0 có ít nhất hai nghiệm.
