DT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
15 tháng 5 2017
Chọn C
Ta có
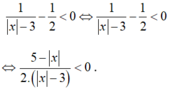
Đặt 
bpt trở thành 
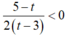
Bảng xét dấu
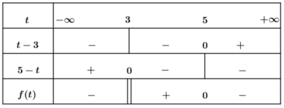
Căn cứ bảng xét dấu ta được
D
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
\(\left|2x-5\right|-3\le0\)
\(\Leftrightarrow\left|2x-5\right|\le3\)
\(\Leftrightarrow-3\le2x-5\le3\)
\(\Leftrightarrow1\le x\le4\)
D
2
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2022
\(\left|2x-5\right|-3\le0\)
\(\Leftrightarrow\left|2x-5\right|\le3\)
\(\Leftrightarrow-3\le2x-5\le3\)
\(\Leftrightarrow1\le x\le4\)
\(\Rightarrow x\in\left[1;4\right]\) (và các tập con của nó)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
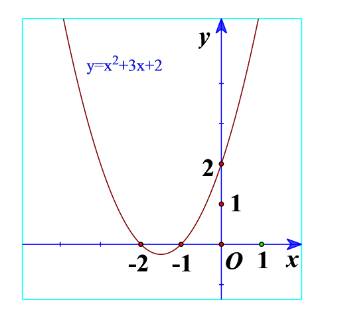
a) Ta thấy trên \(\left( { - \infty ; - 2} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - \infty ; - 2} \right)\)
Trên \(\left( { - 2; - 1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 < 0\)\(\forall x \in \left( { - 2; - 1} \right)\)
Trên \(\left( { - 1; + \infty } \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = {x^2} + 3x + 2 > 0\)\(\forall x \in \left( { - 1; + \infty } \right)\)
b)
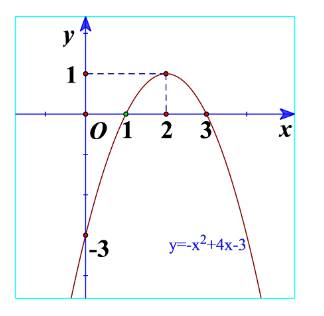
Trên \(\left( { - \infty ;1} \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( { - \infty ;1} \right)\)
Trên \(\left( {1;3} \right)\): Đồ thị nằm trên trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 > 0\)\(\forall x \in \left( {1;3} \right)\)
Trên \(\left( {3; + \infty } \right)\): Đồ thị nằm dưới trục hoành
=> \(f\left( x \right) = - {x^2} + 4x - 3 < 0\)\(\forall x \in \left( {3; + \infty } \right)\)
c) Nếu \(\Delta > 0\) thì \(f\left( x \right)\) cùng dấu vưới hệ số a với mọi x thuộc các khoảng \(\left( { - \infty ;{x_1}} \right)\) và \(\left( {{x_2}; + \infty } \right)\); \(f\left( x \right)\) trái dấu với hệ số a với mọi x thuộc khoảng \(\left( {{x_1};{x_2}} \right)\), trong đó \({x_1},{x_2}\) là hai nghiệm của \(f\left( x \right)\) và \({x_1} < {x_2}\).
PT
1
DT
Đỗ Thanh Hải
CTVVIP
6 tháng 3 2021
Xét f(x) = \(x\left(x^2-1\right)=x\left(x-1\right)\left(x+1\right)\)
f(x) = 0 khi x = 0 hoặc x = 1 hoặc x = -1
Ta có bảng
x \(-\infty\) -1 0 1 \(+\infty\)
x - | - 0 + | +
x-1 - | - | - 0 +
x+1 - 0 + | + | +
f(x) - 0 + 0 - 0 +
=> f(x) \(\ge0\Leftrightarrow x\in\left[-1;0\right]\cup\left[1;+\infty\right]\)
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
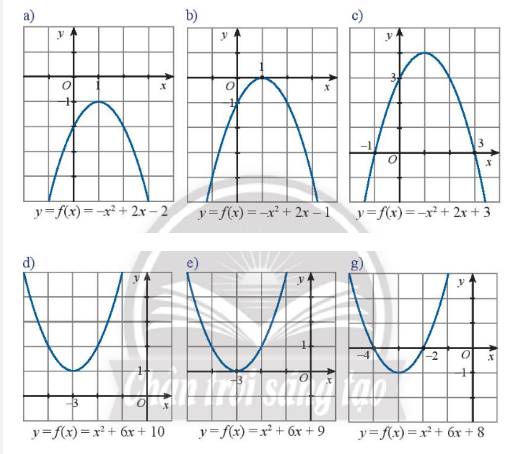
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 2} \right) = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = 1\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 1} \right) = 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 1;{x_2} = 3\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).3 = 16 > 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
Đồ thị nằm trên trục hoành với mọi \(x \in \left( { - 1,3} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm
Biệt thức \(\Delta = {6^2} - 4.1.10 = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi \(x\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = - 3\)
Biệt thức \(\Delta = {6^2} - 4.1.9 = 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 4;{x_2} = - 2\)
Biệt thức \(\Delta = {6^2} - 4.1.8 = 4 > 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
Đồ thị nằm dưới trục hoành với mọi \(x \in \left( { - 4, - 2} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
CM
9 tháng 4 2018
Chọn D.
Nhị thức f(x) nhận giá trị âm với mọi x > -3/2. Do đó, phương trình f(x) = 0 có nghiệm x = -3/2, loại đáp án A và B.
Vì nhị thức f(x) nhận giá trị âm với mọi x > -3/2 nên hệ số a < 0
BN
1
13 tháng 2 2018
\(f\left(x\right)=\left(1-x\right)\left(-x^2+4x-8\right)\)
ta có : \(-x^2+4x-8=-\left(x^2-4x+8\right)=-\left(x^2-4x+4+4\right)\)
\(=-\left[\left(x-2\right)^2+4\right]=-\left(x-2\right)^2-4\le-4< 0\forall x\)
\(\Rightarrow\) \(f\left(x\right)=0\Leftrightarrow1-x=0\Leftrightarrow x=1\)
\(f\left(x\right)>0\Leftrightarrow1-x< 0\Leftrightarrow x>1\)
\(f\left(x\right)< 0\Leftrightarrow1-x>0\Leftrightarrow x< 1\)
vậy ...........................................................................................
(-1; +\infty )(−1;+∞)
(-\infty ; -2)(−∞;−2)
(-2; +\infty )(−2;+∞)
(-2; -1 )(−2;−1)