Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đường vừa nhận được là đường “màu đỏ” trong Hình 7.17.
b) Tổng khoảng cách từ đẩu bút đến các vị trí không thay đổi.

Chọn hệ tọa độ Oxy với gốc tọa độ tại điểm trên của thanh ngắn giữa cầu, trục tung tương ứng là mặt đường của cầu, vẽ lại hình như dưới đây
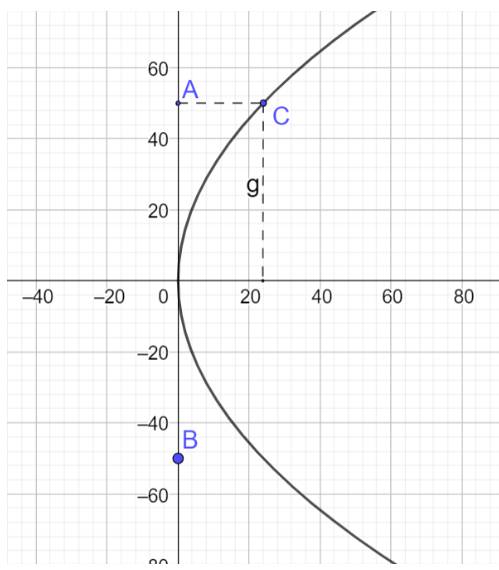
Ta nhận thấy cầu có dạng parabol nên gọi phương trình mô tả hình dạng cầu là \({y^2} = 2px\)
Cầu dài 100 m tương ứng \(AB = 2OB = 100 \Rightarrow OB = 50\), thanh dài nhất dài 30 m
Từ đó ta có tọa độ điểm \(C(24;50)\)
Thay tọa độ C vào phương trình \({y^2} = 2px\) ta có \(2500 = 2p.24 \Rightarrow p = \frac{{625}}{{12}}\)
Ta có phương trình mô tả cây cầu là \({y^2} = \frac{{625}}{6}x\)
Tại thanh cách điểm giữa cầu 18m thì \(x = 18\) ta có \({18^2} = \frac{{625}}{6}.x \Rightarrow x \approx 3,11\)
Do thanh ngắn nhất là 6m nên chiều dài của thanh cách điểm giữa cầu 18m là x + 6 = 3,11+ 6 = 9,11 (m).
Vậy chiều dài của thanh cách điểm giữa cầu 18m gần bằng 9,11 m.

Gọi \(y = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là thành cầu.
Chọn hệ trục tọa độ Oxy như hình dưới:
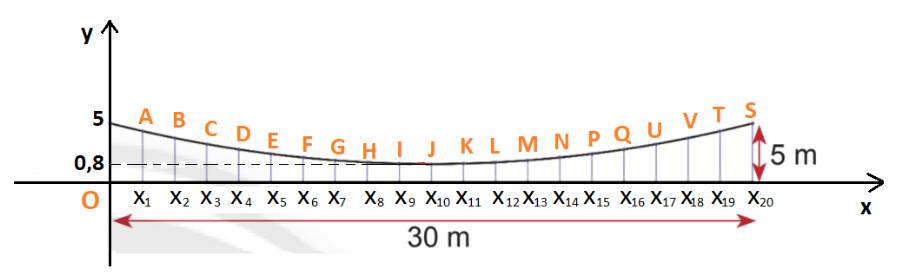
Khi đó độ dài dây cáp dọc ở mỗi mặt bên là tung độ của điểm biểu diễn tương ứng.
Ở mỗi mặt: có 21 dây cáp dọc, tương ứng cho 20 khoảng cách giữa chúng.
Khoảng cách giữa hai dây cáp liền kề là: \(30:20 = 1,5\left( m \right)\)
Khi đó: \({x_0} = 0;{x_1} = 1,5;\;{x_2} = 3;\;{x_3} = 4,5;\;...;{x_n} = 1,5.n\;\)
Dễ thấy: các điểm có tọa độ (0; 5), (\({x_{10}};0,8\)), \(({x_{20}};5)\) thuộc đồ thị hàm số.
(Trong đó: \({x_{10}} = 10.1,5 = 15;\;{x_{20}} = 20.1,5 = 30.\))
Suy ra:
\(f(0) = a{.0^2} + b.0 + c = 5 \Leftrightarrow c = 5\)
Và \(f(1) = a{.15^2} + b.15 + c = 0,8 \Leftrightarrow 225a + 15b + 5 = 0,8\)
\(f(2) = a{.30^2} + b.30 + c = 5 \Leftrightarrow 900a + 30b + 5 = 5\)
Giải hệ phương trình \(\left\{ \begin{array}{l}225a + 15b + 5 = 0,8\\900a + 30b + 5 = 5\end{array} \right.\) ta được \(a = \frac{{7}}{{375}};b = - \frac{{14}}{{25}}\)
Như vậy \(y = \frac{{7}}{{375}}{x^2} - \frac{{14}}{{25}}x + 5\)
Gọi \({y_0},{y_1},{y_2},..{y_{20}}\) là tung độ của các điểm có hoành độ lần lượt là \({x_0},{x_1},{x_2},..{x_{20}}\)
Ta có:
\(\begin{array}{l}{y_0} = 5\\{y_1} = \frac{{7}}{{375}}.1,{5^2} - \frac{{14}}{{25}}.1,5 + 5\\{y_2} = \frac{{7}}{{375}}.{(2.1,5)^2} - \frac{{14}}{{25}}.(2.1,5) + 5 = {2^2}.\frac{{7}}{{375}}.1,{5^2} - 2.\frac{{14}}{{25}}.1,5 + 5\\...\\{y_n} = \frac{{7}}{{375}}.{(n.1,5)^2} - \frac{{14}}{{25}}.(2.1,5) + 5 = {n^2}.\frac{{7}}{{375}}.1,{5^2} - n.\frac{{14}}{{25}}.1,5 + 5\\ \Rightarrow T = {y_0} + {y_1} + {y_2} + .. + {y_{20}} = 5 + \frac{{7}}{{375}}.1,{5^2}.(1 + {2^2} + ... + {20^2}) - \frac{{14}}{{25}}.1,5.(1 + 2 + ... + 20) + 5.20\end{array}\)
Mà \(1 + {2^2} + ... + {20^2} = 2870;\;1 + 2 + ... + 20 = 210\)
\( \Rightarrow T = 5 + \frac{{7}}{{375}}.1,{5^2}.2870 - \frac{{14}}{{25}}.1,5.210 + 5.20 \approx 49,14(m)\)
Do cần tính thêm 5% chiều dài để neo cố định và cần 2 thành mặt cầu nên tổng chiều dài của các dây cáp cần sử dụng là: \(49,14.2.105% = 103,2(m)\)
Vậy chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên là 103,2m.

Khi M thay đổi, hiệu \(M{F_1} - M{F_2} = \left( {M{F_1} + MA} \right) - \left( {M{F_2} + MA} \right) = AB - l{\rm{ }}\)không đổi.

Khi M thay đổi, ta có: \(M{F_1} + M{F_2} +{F_1}{F_2} =\) độ dài vòng dây
⇒ Tổng độ dài \(M{F_1} + M{F_2}\) là một độ dài không đổi (độ dài vòng dây - {F_1}{F_2}).

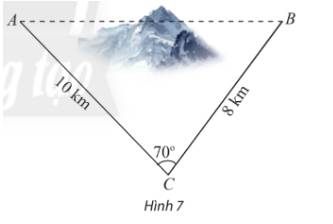
Áp dụng định lí cosin, ta có:
\(\begin{array}{l}A{B^2} = B{C^2} + A{C^2} - 2.BC.AC.\cos C\\ \Leftrightarrow A{B^2} = {8^2} + {10^2} - 2.8.10.\cos {70^o}\\ \Rightarrow AB \approx 10,45\end{array}\)
Vậy chiều dài tăng thêm vì không thể nối trực tiếp là:
\(AC + CB - AB = 10 + 8 - 10,45 = 7,55\;(km).\)



Gọi \(y = f(x) = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là hình ảnh của bộ phận chống đỡ.
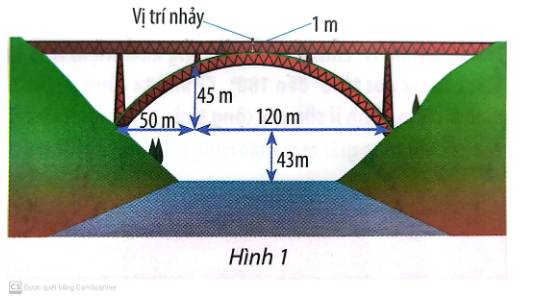
Chọn hệ trục tọa độ Oxy như hình dưới:
Gọi S là đỉnh của parabol, dưới vị trí nhảy 1m.
A, B là các điểm như hình vẽ.
Dễ thấy: A (50; 45) và B (120+50; 0) = (170; 0).
Các điểm O, A, B đều thuộc đồ thị hàm số.
Do đó:
\(f(0) = a{.0^2} + b.0 + c = 0 \Leftrightarrow c = 0\)
\(f(50) = a{.50^2} + b.50 + c = 45 \Leftrightarrow a{.50^2} + b.50 = 45\)
\(f(170) = a{.170^2} + b.170 + c = 0 \Leftrightarrow a{.170^2} + b.170 = 0 \Leftrightarrow a.170+ b = 0\)
Giải hệ phương trình \(\left\{ \begin{array}{l}a{.50^2} + b.50 = 45\\a.170 + b = 0\end{array} \right.\) ta được \(a = - \frac{{3}}{{400}};b = \frac{{51}}{{40}}\)
Vậy \(y = f(x) = - \frac{{3}}{{400}}{x^2} + \frac{{51}}{{40}}x\)
Đỉnh S có tọa độ là \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - \frac{{51}}{{40}}}}{{2.\left( { - \frac{{3}}{{400}}} \right)}} = 85;\;{y_S} = - \frac{{3}}{{400}}.8{5^2} + \frac{{51}}{{40}}.85 = \frac{{867}}{{16}} \approx 54,2\)
Khoảng cách từ vị trí bắt đầu nhảy đến mặt nước là: \(1 + 54,2 + 43 = 98,2(m)\)
Vậy chiều dài của sợi dây đó là: \(98,2:3 \approx 32,7\,(m)\)