Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
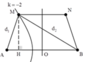
Số điểm dao động với biên độ cực đại trên AB
- A B λ ≤ k ≤ A B λ ⇔ - 8 ≤ k ≤ 8
Để diện tích AMNB là lớn nhất thì M phải nằm trên cực đại ứng với k=-2
d 1 - d 2 = - 2 k λ = - 2 c m .
Mặc khác d 1 2 = A H 2 + M H 2 d 2 2 = B H 2 + M H 2 ⇒ d 1 + d 2 = B H 2 - A H 2 2 = 16 c m
Ta tính được d 1 = 7 c m từ đó suy ra M H = 2 5 c m .
Diện tích hình thang S A M N B = 1 2 A B + M N M H = 18 5 c m 2 .

Chọn đáp án A
+ Bước sóng của sóng λ = 2 πv ω = 4 cm
Độ lệch pha giữa O so với nguồn Δφ = πAB λ = π 2 → O luôn vuông pha với nguồn, vậy các điểm cùng pha với O hiển nhiên sẽ vuông pha với nguồn.
+ Xét tỉ số n = 2 AB λ = 5 → trên đoạn AB có 5 “bó sóng” vớ O là bụng của bó trung tâm. Các bó đối xứng nhau qua một bụng thì cùng pha → có hai điểm khác cùng pha với O.

Đáp án D
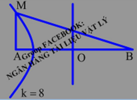
Bước sóng: λ = v f = 40 20 = 2 c m
Vì hai nguồn ngược pha nên điều kiện cực đại cho M là: M A − M B = k + 0 , 5 λ = 2 k + 1
Vì M gần A nhất nên M phải thuộc cực đại ngoài cùng về phía A.
Số cực đại trên AB: − A B λ − 1 2 < k < A B λ − 1 2
⇒ − 8 , 5 < k < 8 , 5 ⇒ k = − 8 ⇒ M A − M B = 2 − 8 + 1 = − 15 ⇒ M B = M A + 15 1
Vì Δ A M B vuông tại A nên: M A 2 + A B 2 = M B 2 2
Thay (1) vào (2) ta có: M A 2 + 16 2 = M A + 15 2 ⇒ M A = 1 , 03 c m








Đáp án B
M cực đại nên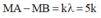
M gần B nhất nên k phải max.
Ta có
Vì k max nên chọn k = 3. Suy ra MA-MB=15. Lại có
Vậy x = 3,3 thỏa mãn đề bài