Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử khoảng cách AB = d (km).
Gọi vận tốc của người đi bộ là x km/h, x > 0.
Theo đầu bài, người đi ngựa đi quãng đường AB hết 5/6 giờ. Do đó vận tốc của người đi ngựa là d: 5/6 = 6d/5 (km).
Người đi ngựa đến trước người đi bộ 5/6 giờ. Điều đó có nghĩa là
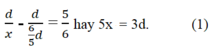
Từ đó cũng suy ra 6d/5 = 2x; nghĩa là vận tốc của người đi ngựa là 2x km/h. Vì người đi ngựa khi quay lại gặp người đi bộ ở điểm cách B một khoảng là 2km nên:
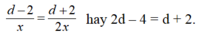
Từ (1) và (2), ta có hệ phương trình 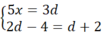
Giải hệ này ta được d = 6, x = 3,6.
Vậy: Khoảng cách AB = d = 6 km,
Vận tốc của người đi bộ là 3,6 km/h,
Vận tốc của người đi ngựa là 7,2 km/h.

Gọi khoảng cách giữa hai bản A và B là x (km)
Vận tốc của người đi bộ là y (km/h)
Điều kiện: x > 0; y > 0
Người đi ngựa cả đi và về hết 1 giờ 40 phút =53=53 giờ nên người đi ngựa đi từ A đến B hết 53:2=5653:2=56 giờ.
Vận tốc của người đi ngựa bằng x:56=65xx:56=65x (km/h)
Thời gian người đi bộ đi hết quãng đường AB là xyxy giờ
Người đi ngựa đến trước 50 phút =56=56 giờ, ta có phương trình:
xy−56=56⇔3x=5yxy−56=56⇔3x=5y (1)
Từ (1) ⇒ 6x=10y⇔65x=2y.6x=10y⇔65x=2y. Điều này có nghĩa là vận tốc người đi ngựa gấp đôi người đi bộ nên vận tốc người đi ngựa là 2y (km/h).
Từ lúc đi đến lúc gặp nhau người đi bộ đi được x – 2 (km), người đi ngựa đi được x + 2 (km).
Vì từ lúc đi đến lúc gặp thời gian hai người bằng nhau, ta có phương trình:
x−2y=x+22y⇔2x−4=x+2x−2y=x+22y⇔2x−4=x+2
Ta có hệ phương trình:
{3x=5y2x−4=x+2⇔{3x=5yx=6⇔{3.6=5yx=6⇔{x=6y=3,6{3x=5y2x−4=x+2⇔{3x=5yx=6⇔{3.6=5yx=6⇔{x=6y=3,6
x = 6 và y = 3,6 thỏa mãn điều kiện bài toán.
Vậy khoảng cách giữa hai bản là 6km
Vận tốc người đi bộ là 3,6 km/h
Vận tốc người đi ngựa là 7,2 km/h


a, có s1=s2
Vận tốc người 1 là : \(v_{tb}=\frac{s_1+s_2}{t_1+t_2}=\frac{2}{\frac{1}{v_1}+\frac{1}{v_2}}=\frac{2}{\frac{1}{12}+\frac{1}{8}}=9,6\left(\frac{km}{h}\right)\)
Vận tốc người 2 là :\(v_{tb}=\frac{s_1+s_2}{t_1+t_2}=\frac{2}{\frac{1}{v_1}+\frac{1}{v_2}}=\frac{2}{\frac{1}{8}+\frac{1}{12}}=9,6\left(\frac{km}{h}\right)\)
=>2 người đến lúc cùng nhau cùng vận tốc 9,6 km/h
b, chắc đề sai vì 2 người đến cùng lúc mà

Gọi \(x\left(km/h\right)\) là vận tốc lúc đi và lúc về \(\left(x>0\right)\)
\(x+10\) là vận tốc lúc về \(\left(km/h\right)\)
Đổi \(2h12p=2,2h\)
Theo đề, ta có pt :
\(\dfrac{60}{x}+\dfrac{60}{x+10}=2,2\)
\(\Leftrightarrow60\left(x+10\right)+60x-2,2x\left(x+10\right)=0\)
\(\Leftrightarrow60x+600+60x-2,2x^2-22x=0\)
\(\Leftrightarrow-2,2x^2+98x+600=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=50\left(tmdk\right)\\x=-\dfrac{60}{11}\left(ktmdk\right)\end{matrix}\right.\)
Vậy vận tốc lúc đi là \(50km/h\)
lúc về là : \(50+10=60\left(km/h\right)\)

